Пучок плоскостей

Пучком плоскостей называют — множество всех плоскостей, проходящих через одну и ту же прямую KM (где KM — общая линия (прямая) пересечения плоскостей также называют её  осью пучка см. рисунок ниже).

 
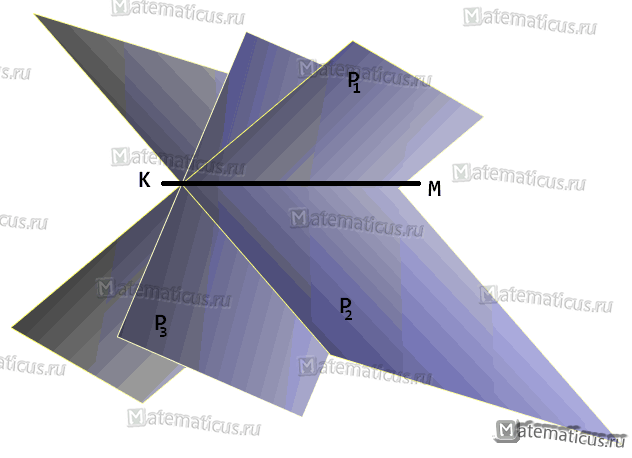
Если известны уравнения двух различных плоскостей P₁ и P₂ 

  A₁x+B₁y +C₁z+D₁=0  
  А₂х+В₂у+C₂z+D₂=0  

принадлежащих пучку, то каждую плоскость пучка можно представить уравнением вида:

   m₁⋅(A₁x+B₁y+C₁z+D₁)+m₂⋅( А₂х+В₂у+C₂z+D₂)=0

  Это уравнение называется уравнением пучка плоскостей
Когда m₁≠0, можно разделить уравнение на m₁. Обозначив m₁:m₂ через λ, получим уравнение:

A₁x+B₁y+C₁z+D₁+λ⋅( А₂х+В₂у+C₂z+D₂)=0 

---

Пример 1
Даны уравнения
5х-3у=0  и  3z-4x=0
Уравнение пучка есть:
m₁⋅(5х-3у) + m₁⋅(3z-4x )=0
Например, взяв  m₁=1,  m₂=-2, будем иметь:
1⋅(5х-3у) + (-2)⋅(3z-4x )=0
Отсюда получаем:
13x-3y-6z=0
Уравнение представляет одну из плоскостей пучка.

---

Пример 2
Найти уравнения проекции прямой T
2x+3y+4z+5=0, x-6y+3z-7=0
на плоскость P
2x+2y+z+15=0

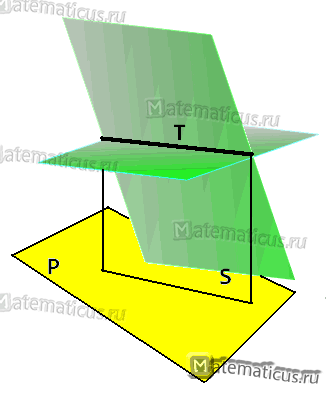
Решение

Искомая проекция представляется уравнением вида:
(2x+3y+4z+5)+λ⋅(x-6y+3z-7)=0

Чтобы найти λ, представим в виде:
(2+λ)⋅х+(3-6λ)⋅у+(4+3λ)⋅z+5-7λ=0 (1)
и запишем условие перпендикулярности плоскостей:

Подставляя A=2, B=2, C=1, получаем:
2⋅(2+λ)+2⋅(3-6λ)+1⋅(4+3λ)=0
Отсюда  λ=2. Подставляя  λ=2 в уравнение (1), получим уравнение плоскости S. Искомая проекция  представляется уравнениями:

4x-9y+10z-9=0

2x+2y+z+15=0