Обозначение скалярного произведения: a·b или ab или (a, b), на письме пишется со стрелочкой, т.е. $\vec a\vec b$

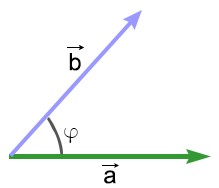
Скалярное произведение вектора а на вектор b называется произведение их модулей (длин) на косинус угла между ними, т.е.

  a·b =|a|·|b|·cos(a,^b)

или

a·b =|a|·|b|·cos(φ)

a·b>0 — угол острый между векторами;
a·b<0 — угол тупой между векторами;
a·b=0 — угол прямой между векторами.

Примечание
Скалярное умножение не распространяется на случай трёх сомножителей.

---

Физический смысл скалярного произведения 

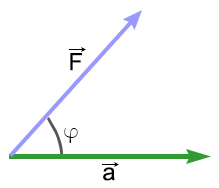
Физический смысл скалярного произведения заключается в том, что работа А равна произведению производимой постоянной силой F при перемещении тела на вектор a и составляющий с направлением силы F угол φ. Эта связь выражается формулой:

  A = |F|·|a|=|F|·|a|·cosφ

A — работа, скалярная величина;
a — вектор перемещения (смещения) материальной точки;
F — вектор силы действующий на эту точку;
φ — угол силы F действующий к смещению a

---

Пример 1 
Длины векторов a и b соответственно равны 3 м и 2 м, а угол между ними 120⁰.
Найти скалярное произведение a·b.

  Решение 

a·b=|a|·|b|·cos(a,^b)=3·2·cos(120⁰)=−3 м² 

---

Пример 2 
Длины вектор силы F имеет модуль 4 кг, длина вектора смещения а равна 2 м. Пусть сила F действует под углом φ=60⁰ к смещению a.

Найти работу силы.

  Решение 
F·a=|F|·|a|·cosφ=4·2·cos(60⁰)=4·2·0.5=4 м²