Сложение векторов
Сложение векторов по правилу параллелограмма
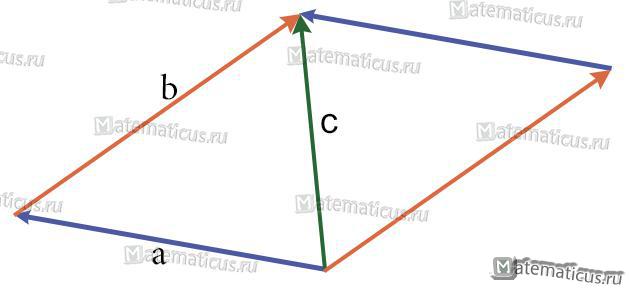
Правило параллелограмма
Если слагаемые a и b не коллинеарны, то
c=a+b
Сложение векторов по правилу треугольника
Правило треугольника
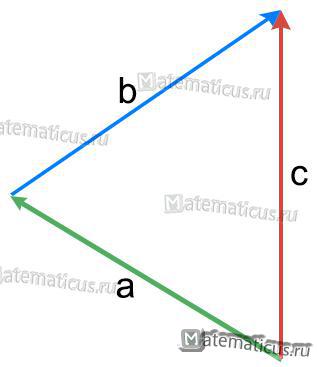
Суммой векторов a (на рисунке зелёный вектор) и b (на рисунке синий вектор) называется третий вектор c (на рисунке красный вектор) , получаемый следующее построение:
Примечание
Нельзя смешивать понятие «сумма отрезков» с понятием «сумма векторов».
Правило параллелепипеда
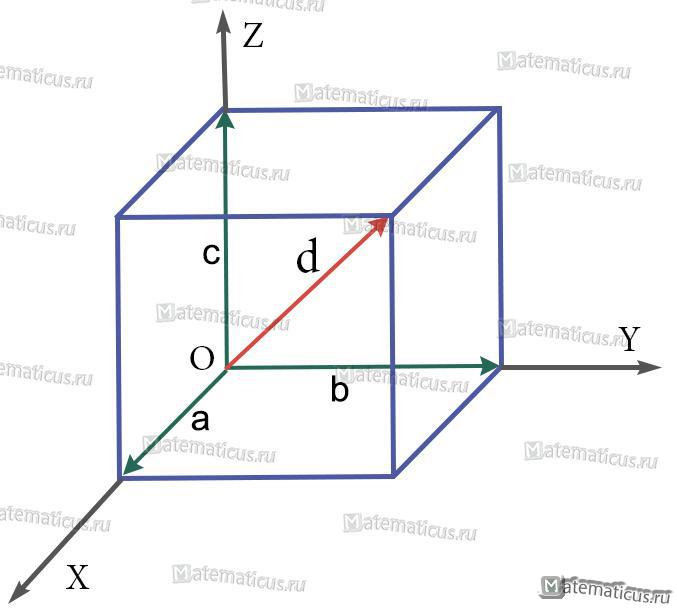
Если три вектора a, b, c после приведения к общему началу не лежат в одной плоскости , то их сумма равна диагонали параллелепипеда
d=a+b+c
Правило параллелепипеда применяется для сложения трех некомпланарных векторов.
Сложение противоположных векторов
Сумма противоположных векторов равна нуль-вектору, т.е.

a+(-a)=0
Свойство переместительности (переместительный закон)

От перестановки слагаемых сумма векторов не меняется.
с=a+b= b+a
Сочетательное свойство (сочетательный закон)
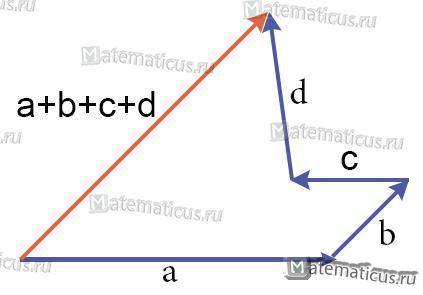
Слагаемые векторы можно группировать как угодно.
a+(b+c+d) = a+b+c+d
Вычитание векторов
Вычесть вектор а (вычитаемое) из вектора b (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором а даёт вектор b.
Разность векторов обозначается: a-b
Вычитание есть действие обратное сложению (сложение векторов).
Вычитание векторов показаны на рисунках ниже:
Примечание
Модуль разности может быть меньше модуля «уменьшаемого», но может быть и больше или равен ему. Эти случаи показаны на рисунке выше.
