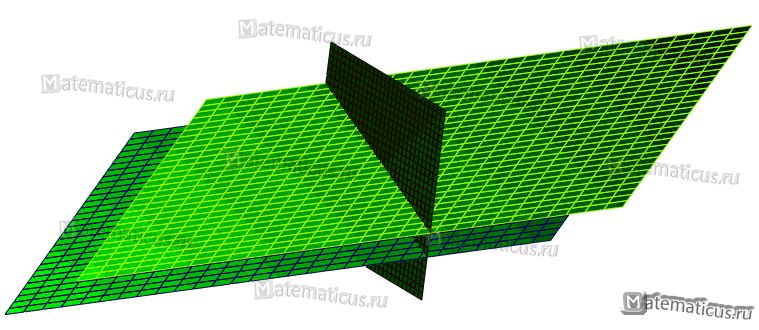
Чтобы найти координаты точки пересечения трех плоскостей, необходимо решить эти уравнения относительно х, у и z, при этом координаты точки пересечения должны удовлетворять уравнениям всех трех плоскостей.
Система уравнений трёх плоскостей имеет вид:
A1x + B1y + C1z + D1 = 0
A2x + B2y + C2z + D2 = 0
A3x + B3y + C3z + D3 = 0
Если определитель этой системы не равен нулю,
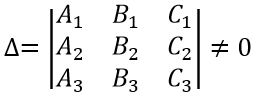
то система имеет единственное решение и тогда три плоскости пересекаются в одной точке.
Замечания
1. Если три плоскости не имеют ни одной общей точки ( или хотя бы две из них параллельны) — система уравнений не имеет решений.
2.Если плоскости имеют бесчисленное множество общих точек ( все они проходят через одну прямую), то система уравнений имеет бесчисленное множество решений.
3.Если система имеет одну общую точку, то система уравнений имеет только одно решение.
Пример 1
Исследовать, есть ли общие точки у плоскостей
x+y+z=1, x-2y-3z=5, 2x-y-2z=6
Оно имеет бесчисленное множество решений. Значит, три плоскости имеют бесчисленное множество общих точек, т. е. проходят через одну прямую.
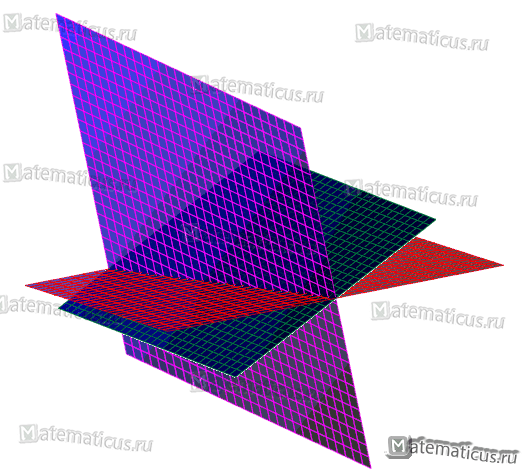
Пример 2
х-у+2=0
х+2у-1=0
x+y-z+2=0
Решая эти уравнения совместно, получим координаты искомой точки x=-1; y=1; z=2.
Таким образом плоскости имеют одну общую точку (-1; 1; 2), так как система уравнений имеет единственное решение.

Пример 3
Плоскости
4х-2у+z-4=0 (1)
8х-4у+2z+9=0 (2)
x+y-5z=0 (3)
не имеют общих точек, так как плоскости (1) и (2) параллельны.
Система уравнений несовместима (уравнения (1) и (2) противоречат друг другу).