Углом φ между векторами, по сути, это наименьший угол, образуемый векторами при совмещении их начал.
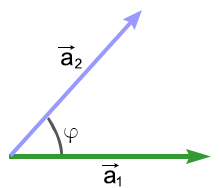
Угол φ между векторами a1{X1;Y1;Z1} и a2{X2;Y2;Z2} находится по формуле:
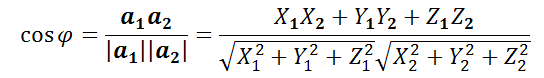
Пример
Найти угол между векторами a1{1;2;-1} и a2{3;-1;-2}
Решение
Подставляя в формулу выше, получаем
$\cos \varphi = \frac{{{a_1}{a_2}}}{{\left| {{a_1}} \right|\left| {{a_2}} \right|}} = $
$=\frac{{{X_1}{X_2} + {Y_1}{Y_2} + {Z_1}{Z_2}}}{{\sqrt {X_1^2 + Y_1^2 + Z_1^2} \sqrt {X_2^2 + Y_2^2 + Z_2^2} }} = $
$ = \frac{{1·3 + 2·\left( { — 1} \right) + \left( { — 1} \right)·\left( { — 2} \right)}}{{\sqrt {{1^2} + {2^2} + {{\left( { — 1} \right)}^2}} \sqrt {{3^2} + {{\left( { — 1} \right)}^2} + {{\left( { — 2} \right)}^2}} }} = $
$=\frac{3}{{\sqrt {84} }} \approx 0,32$
Отсюда получаем угол φ
φ=70.890
