Уравнение плоскости проходящей через точку и прямую

Плоскость, проходящая через данную точку М₀(х₀;у₀;z₀) и через данную прямую K (плоскость проходит через прямую):

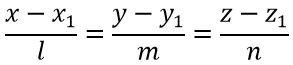
и не проходящую через точку М₀, представляется уравнением (1):

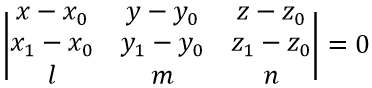
Эта запись в векторной форме (2):

(r−r₀)(r₁−r₀)а = 0  

Уравнение  (1) или (2)  выражает  компланарность   векторов а{l,m,n}
и $\overrightarrow {{M_0}M} $, $\overrightarrow {{M_0}{M_1}} $

Примечание
Если прямая K проходит через точку М₀, то уравнение (1) становится тождеством и, следовательно, задача имеет бесчисленное множество решений.

---

Пример
Плоскость,    проходящая    через    точку М₀(5;2;3) и прямую

$\frac{{x + 1}}{2} = \frac{{y + 1}}{1} = \frac{{z — 5}}{3}$

представляется уравнением:

$\left| {\begin{array}{*{20}{c}}{x — 5}&{y — 2}&{z — 3} \\  { — 6}&{ — 3}&2 \\  2&1&3 \end{array}} \right| = 0$

получаем

x-2y-1=0