Если плоскости
A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0
параллельны, то и их нормальные векторы (нормали) параллельны (коллинеарны), т.е.
N1{A1;B1;C1} // N2{A2;B2;C2},
тогда условие параллельности плоскостей запишем:
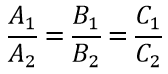
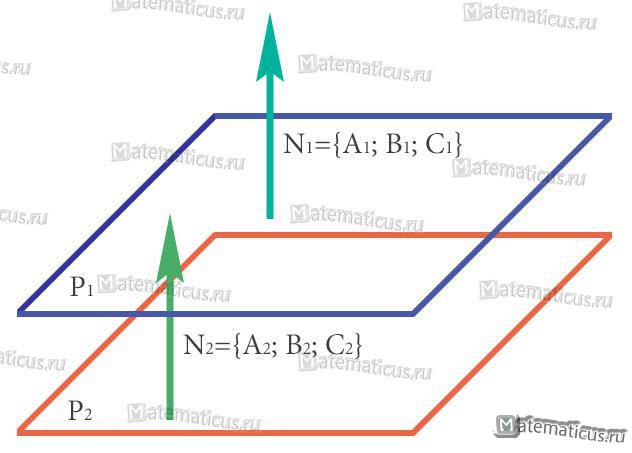
Примечание
Если
$\frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}} = \frac{{{D_1}}}{{{D_2}}}$
то плоскости совпадают
Пример
Плоскости 2x-3y-4z+11=0 и -4x+6y+8z+36=0 параллельны, так как
$\frac{{ — 4}}{2} = \frac{6}{{ — 3}} = \frac{8}{{ — 4}}$