Векторное произведение двух векторов

Векторное произведение двух векторов возникло из понятия момента силы.

Векторным произведением вектора а на не коллинеарный с ним вектор b называется третий вектор с, который строится следующим образом

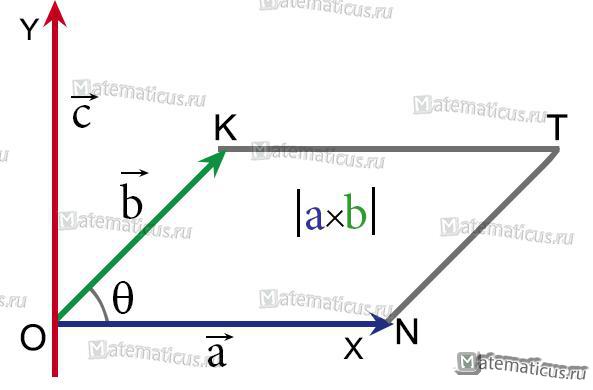
и удовлетворяет следующим условиям:
1) его модуль численно равен площади параллелограмма (NOKT, построенного
векторах а и b, т. е. он равен:

  |c|=|a|·|b|·sin(a,^b)

2) его направление перпендикулярно к плоскости упомянутого параллелограмма;
3) при этом направление вектора с выбирается (из двух возможных) так, чтобы векторы a, b, с составляли правую систему.

---

Геометрический смысл векторного произведения

Модуль векторного произведения двух векторов численно равен площади параллелограмма, построенного на этих векторах, т.е.

$\left| {\vec a \times \vec b} \right| = {S_{параллелограмма}}$

---

Векторное произведение двух трехмерных векторов, заданных в координатной форме 

Векторное произведение двух трехмерных векторов a={x₁,y₁,z₁} и b={x₂,y₂,z₂}, заданных в координатной форме определяется по формуле:

---

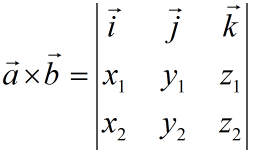
Пример 1

Найти векторное произведение двух векторов a={x₁,y₁,z₁} и b={x₂,y₂,z₂}, заданных в координатной форме

Решение

Подставляя в формулу выше, находим векторное произведение векторов

$\vec a \times \vec b = \left| {\begin{array}{*{20}{c}} {\vec i}&{\vec j}&{\vec k} \\ 2&{ — 1}&1 \\ { — 3}&4&1 \end{array}} \right| =$

$= — 5i — 5j + 5k$

---

Пример 2
Векторы а и b имеют длины, соответственно равные 20 см и 30 см, и образуют угол в 30⁰. Найти длину векторного произведения aхb.

Решение

|a|·|b|·sin(a,^b)=20·30·sin30⁰=

=20·30·0.5=600·0.5=300 см²