Дифференциальное уравнение вида:
y’ + P(x)y = Q(x)
называется линейным дифференциальным уравнением первого порядка.
P(x), Q(x) — непрерывные функции.
Решается уравнение заменой неизвестной функции.
Возьмём производную от функции
y=u·v
получим
y’=u’v+uv’
Подставляем в исходное уравнение, получаем
u’v+uv’+P(x)u·v = Q(x)
отсюда
u’v+u(v’+P(x)v) = Q(x)
Возьмём функцию, которая в скобках дает ноль, запишем так
u(v’+P(x)v)=0
Решая уравнения
v’+P(x)v=0
имеем
v=e-∫P(x)dx
Теперь найдем оставшуюся часть уравнения
u’v= Q(x)
u’e-∫P(x)dx= Q(x)
Отсюда
u=∫Q(x)·e∫P(x)dx dx+C
Тогда общее решение уравнения будет
y=(∫Q(x)·e∫P(x)dx dx+C)·e-∫P(x)dx
Пример 1
Решить уравнение
$$y’ — y = {e^x}$$
Решение
Воспользуемся формулой выше, получим решение
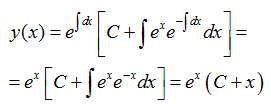
Пример 2
Решить уравнение
$xy{\text{‘}} + y = sin2x$
Решение
Для решения этого уравнения, сделаем подстановку вида
y=u·v
y’=u’v+uv’
Тогда имеем
$x\left( {u’v + uv’} \right) + uv = sin2x$
$xu’v + uv + xuv’ = sin2x$
$v\left( {xu’ + u} \right) + xuv’ = sin2x$
$xu’ + u = 0$
$x\frac{{du}}{{dx}} + u = 0$
$\frac{{du}}{u} = — \frac{{dx}}{x}$
$\mathop \smallint \nolimits^ \frac{{du}}{u} = \mathop \smallint \nolimits^ — \frac{{dx}}{x}$
$\ln \left| u \right| = — {\text{ln}}\left| x \right|$
$u = \frac{1}{x}$
$x\frac{1}{x}v’ = sin2x$
$\frac{{dv}}{x} = sin2x$
$\int {dv = \int {\sin 2xdx} } $
$v = — \frac{1}{2}{\text{cos}}2{\text{x}} + {\text{C}}$
Запишем общее решение уравнения
$y = \frac{1}{x}\left( { — \frac{1}{2}{\text{cos}}2{\text{x}} + {\text{C}}} \right)$
