Задача Коши Пример решения дифференциального уравнения

Задача Коши для дифференциального уравнения — это задача, в которой кроме самого дифференциального уравнения заданы начальные условия. Обычно она формулируется следующим образом: найти функцию y(x), удовлетворяющую дифференциальному уравнению и начальным условиям.

Общая форма задачи Коши для обыкновенного дифференциального уравнения (ОДУ) выглядит следующим образом:

$$\frac{dy}{dx} = f(x, y)$$

$$y(x_0) = y_0$$

где f(x, y) — заданная функция, определяющая дифференциальное уравнение, y(x₀) = y₀ — начальные условия, заданные в точке x₀.

Решение задачи Коши для дифференциального уравнения позволяет найти функцию y(x), которая удовлетворяет уравнению $\frac{dy}{dx} = f(x, y)$ и начальным условиям y(x₀) = y₀.

Существует множество методов для решения задачи Коши для дифференциальных уравнений, включая метод Эйлера, метод Рунге-Кутты, метод стрельбы и другие. Выбор метода зависит от конкретной формы дифференциального уравнения и его начальных условий.

Пример

Задача Коши должна удовлетворять следующим начальным условиям:

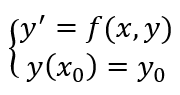
y’=3x²y

y(0)=1

Решение задачи Коши