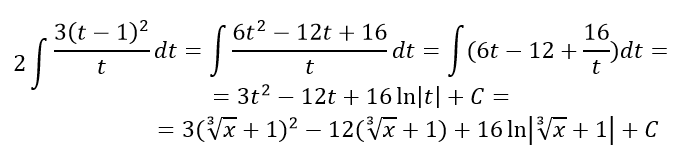Функция называется иррациональной, если переменная величина находится под знаком корня.
Алгоритм решения интеграла иррациональной функции заключается в приведении ее к рациональной функции за счет возведении в степень.
Пример 1
Найти
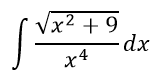
Решение
Выполним преобразование иррациональной функции, возведя в квадрат:
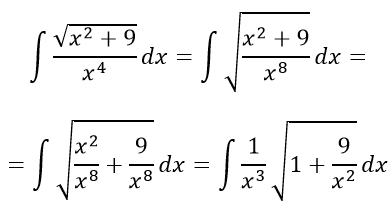
Сделаем подстановку, тогда
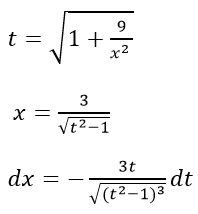
выполним подстановку и преобразуем функцию к удобному виду для интегрирования
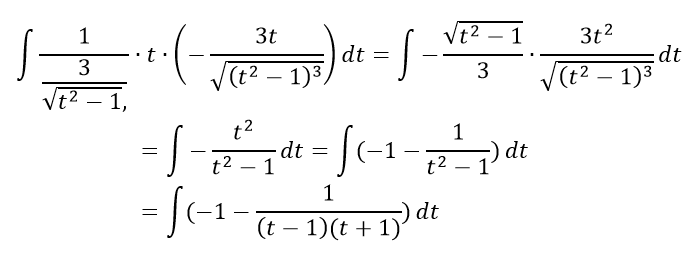
выполним интегрирование рациональной дроби
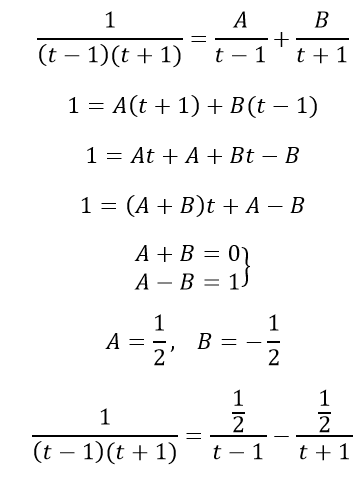
найдем интеграл от иррациональной функции
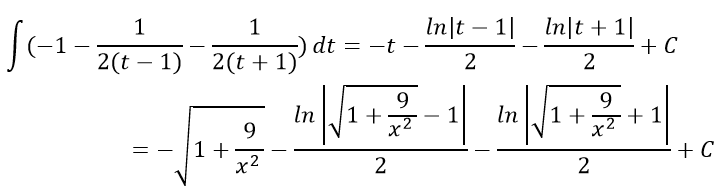
Пример 2
Найти
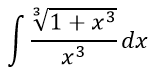
Решение
Преобразуем дробь, возведя в куб
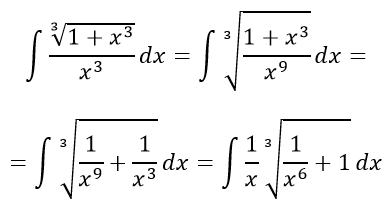
сделаем подстановку, тогда
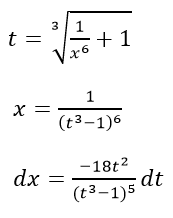
Таким образом, получим интеграл от рациональной дроби
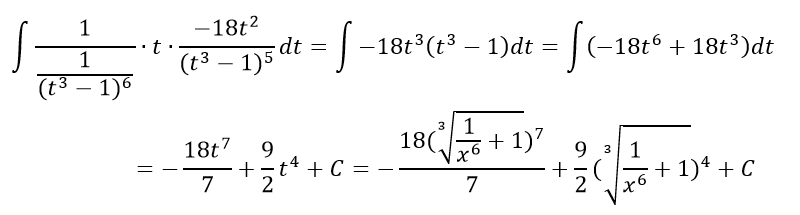
Пример 3
Найти
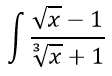
Решение
Выполним преобразование интеграла
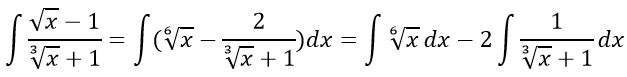
Разобьём интеграл на два интеграла
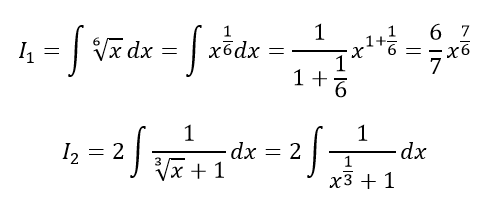
Делаем замену, пусть
$\sqrt[3]{x}+1=t$
$x=(t-1)^3$
$dx=3(t-1)^2 dt$
далее выполняем решение интеграла