Вычисление определенного интеграла методом Симпсона

Методом Симпсона предназначен для численного вычисления определённого интеграла, его также называют методом парабол. Данный метод по точности в десятки раз выше, чем у метода прямоугольников и метода трапеций.

Формула Симпсона для вычисления определённого интеграла:

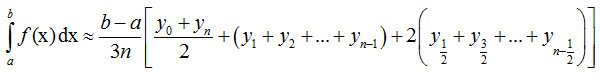
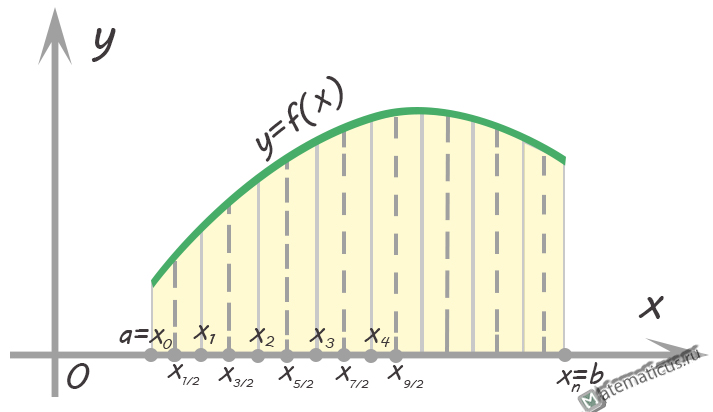
График — метод Симпсона

Погрешность метода Симпсона находится по формуле:

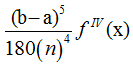
fIV(x) – наибольшее значение производной IV порядка | fIV(x)|, x(a, b)

---

Пример вычисления определённого интеграла по формуле Симпсона

$$\int\limits_0^1 {{e^x}dx} $$

При n=2, получаем

(b-a)/3n=1/6
x₀=0
x₁=0,5
x₂=1
x_1/2=0,25
x_3/2=0,75

y₀=0,5
y₁=1,648721271
y₂=1,359140914
y_1/2=2,568050833
y_3/2=4,234000033

Общая сумма по y равна:

$$\sum  = 10,30991$$

Воспользовавшись формулой Симпсона, получаем решение определённого интеграла

$$I \approx \frac{1}{6}10,30991 = 1,718319$$

Погрешность равна 0,0000370135

Для сравнения точности методов вычисления определённого интеграла см. решения этого же интеграла методом трапеций и методом прямоугольников.

Точное аналитическое решение данного определённого интеграла см.здесь