Вычисление определенного интеграла методом трапеций

Метод трапеций предназначен для вычисления определенных интегралов и относится к численному методу интегрирования.

Формула трапеций для вычисления определённого интеграла имеет вид:

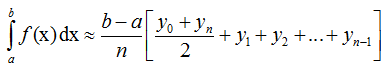
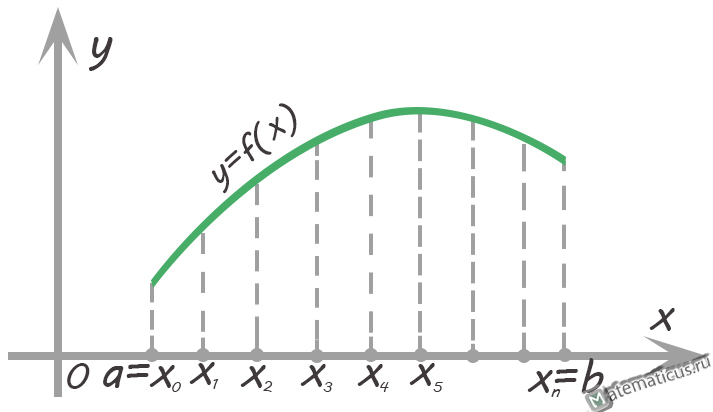
График — метод трапеций

Погрешность значения формулы трапеций вычисляется по формуле:

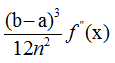
f’’(x) – наибольшее значение производной |f’’(x)|, x(a, b)

---

Пример решения определенного интеграла методом трапеций для функции

$$\int\limits_0^1 {{e^x}dx} $$

Шаг для промежутка от 0 до 1 возьмём 0.1, получим следующие значения x
x₁=0,1
x₂=0,2
x₃=0,3
x₄=0,4
x₅=0,5
x₆=0,6
x₇=0,7
x₈=0,8
x₉=0,9

Далее, эти значения последовательно подставляем в функцию у=e^x, имеем

y₁=1,105170918
y₂=1,221402758
y₃=1,349858808
y₄=1,491824698
y₅=1,648721271
y₆=1,8221188
y₇=2,013752707
y₈=2,225540928
y₉=2,459603111

Применим для вычисления определённого интеграла формулу трапеций, получим численное решение интеграла

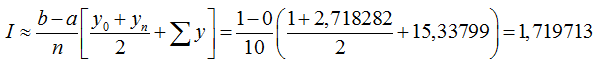
Погрешность равна 0,0014317

Для сравнения точности методов вычисления определённого интеграла см. решения этого же итеграла методом Симпсона и методом прямоугольников.

Точное аналитическое решение данного определённого интеграла см.здесь