Площадь плоских фигур определяется через определённый интеграл от неотрицательной функции и равна площади криволинейной трапеции. В этом также заключается и геометрический смысл определённого интеграла.
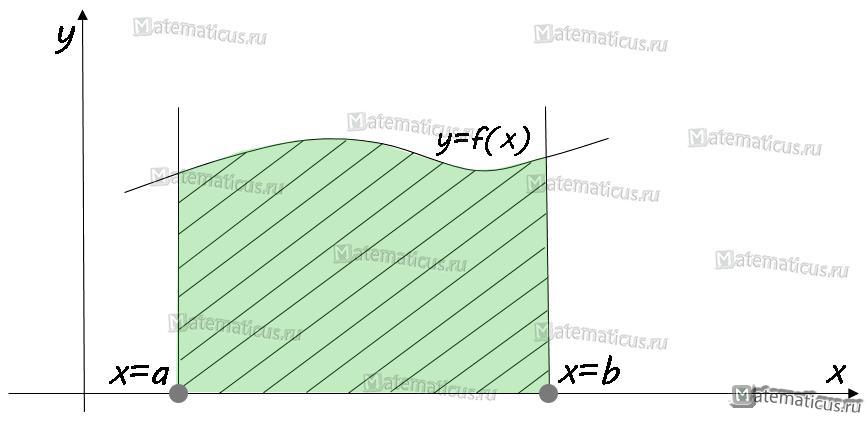
Криволинейной трапецией называется фигура, которая ограничена графиком непрерывной функции f(x)≥0, прямыми x=a, y=b и осью OX.
I. Площадь криволинейной трапеции на оси OX вычисляется по формуле:
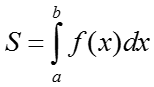
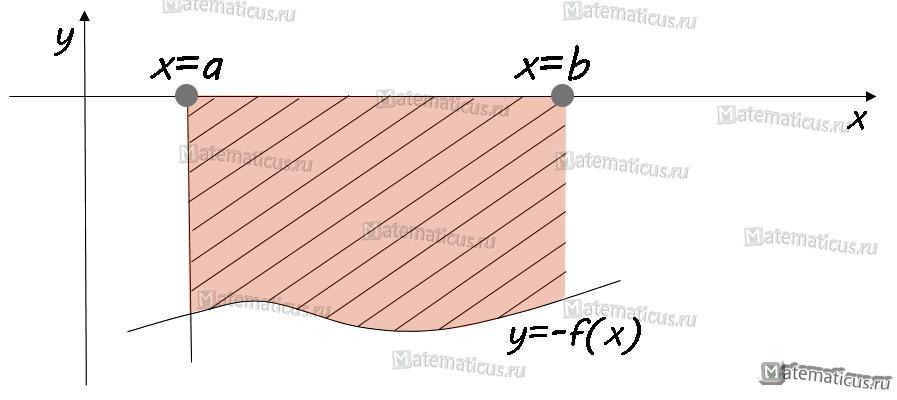
II. Если функция f(x)<0, то криволинейная трапеция находится ниже оси OX и тогда её площадь определяется по формуле:
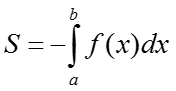
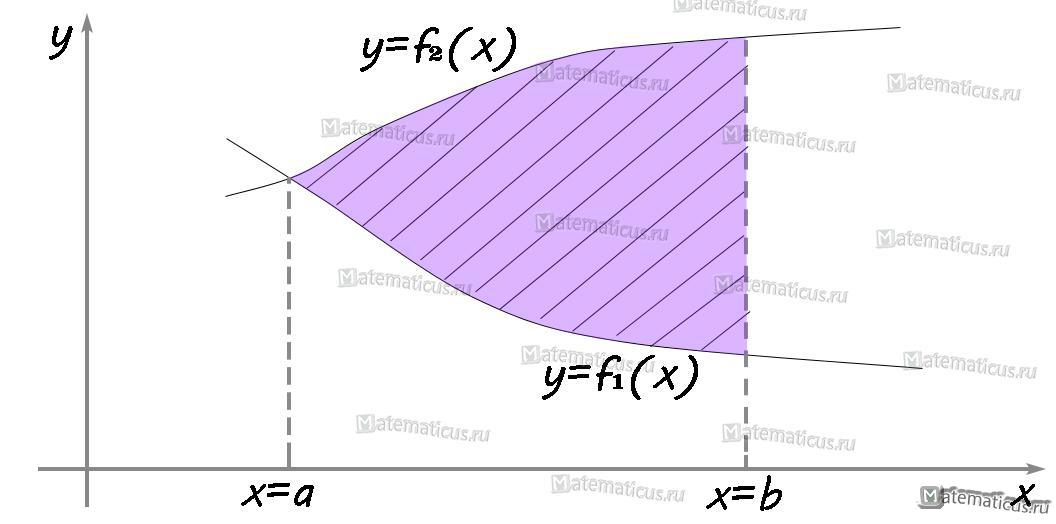
III. Если функция f2(x)≥f1(x), f2(x)-f1(x)≥0 то площадь фигуры находится по формуле:
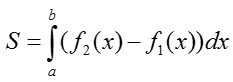
Читается так: из верхней функции вычитаем нижнюю.
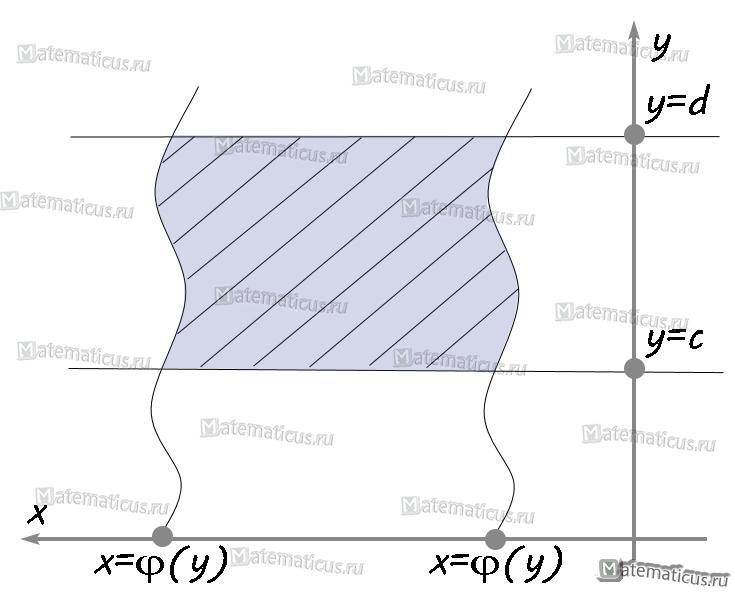
IV. Площадь криволинейной трапеции на оси OY определяется по формуле: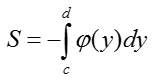
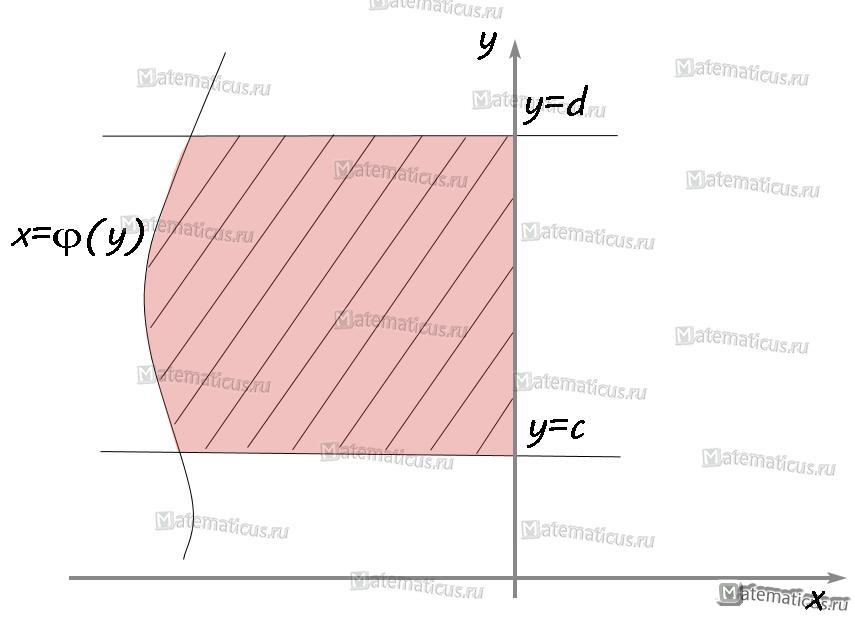
V. Если криволинейная трапеция расположена левее оси OY, то её площадь находится по формуле: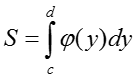
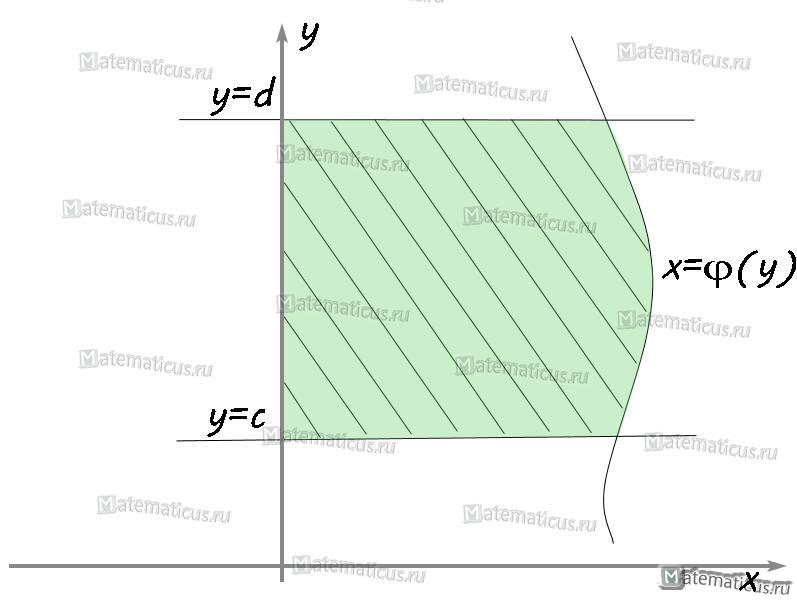
VI. Если функция φ2(x)≥φ1(x), φ2(x)-φ1(x)≥0, то площадь криволинейной трапеции ограниченна графиками x=φ1(x), x=φ2(x) и прямыми y=d, y=c и определяется по формуле:
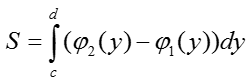
Если плоская фигура не относится к криволинейной трапеции вышеперечисленных видов, то её разбивают прямыми на криволинейные трапеции, которые параллельны оси OX или OY. Затем используют приведённые формулы выше.
Пример 1
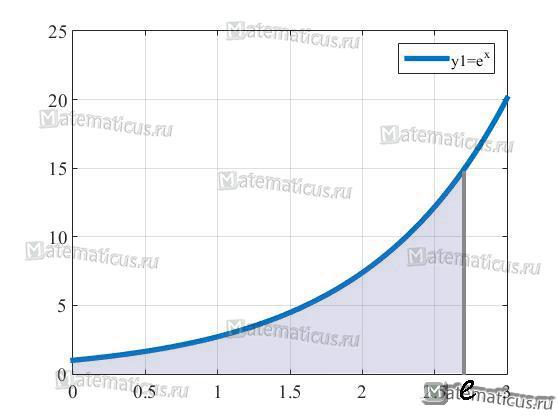
Найти площадь S фигуры, ограниченной функцией f(x)=ex и линиями x=0 и x=e
Решение
Построим график функции f(x)=ex
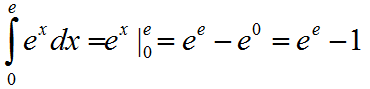
Пример 2
Найти площадь S фигуры, ограниченной линиями y=x2 и y=3x
Решение
Пределами интегрирования являются точки абсциссы пересечения этих функций.
Графически можно представить следующем образом.
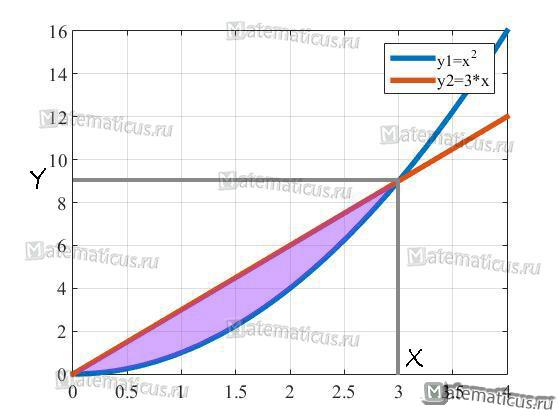
Найдем их через решения системы уравнений.
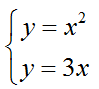
Решая систему находим корни x1=0 и x2=3
$$\eqalign{& \int\limits_0^3 {3x — {x^2}dx = } \cr & = \left( {\frac{3}{2}{x^2} — \frac{1}{3}{x^3}} \right)|_0^3 = \cr & = \frac{{27}}{2} — \frac{{27}}{3} = \frac{{27}}{6} = 4,5 \cr} $$