Вертикальная асимптота

Прямая x=a на графике 1 — вертикальная асимптота.
Если один из пределов $\mathop {\lim }\limits_{x \to {a} — 0} f(x)$ или $\mathop {\lim }\limits_{x \to {a} + 0} f(x)$ равен бесконечности, то это вертикальная асимптота.

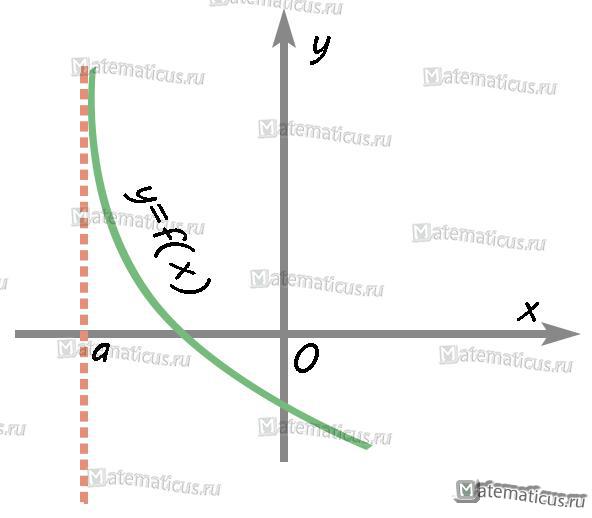
График 1 — вертикальной асимптоты x=a

Горизонтальная асимптота

Прямая (график 2) y=b является горизонтальной асимптотой при условии, если существуют конечные пределы:

$\mathop {\lim }\limits_{x \to  + \infty } f(x) = b$ и $\mathop {\lim }\limits_{x \to  — \infty } f(x) = b$

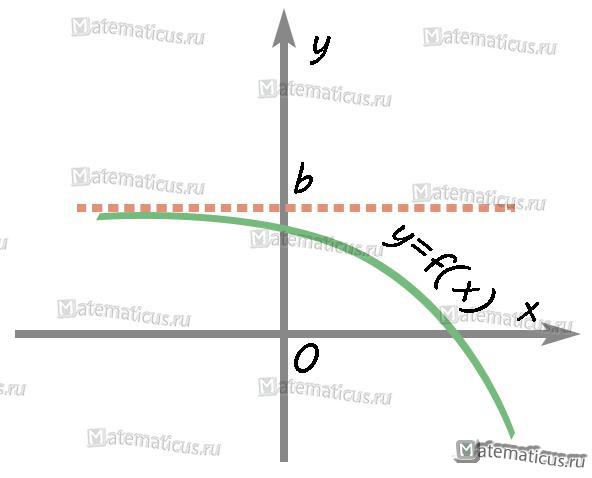
График 2 горизонтальной асимптоты y=b

Наклонная асимптота

Прямая (график 3) y=kx+b является наклонной асимптотой, если существуют конечные пределы k и b при x→∞ или x→+∞:

$k = \lim \frac{{f(x)}}{x}$ и $b = \lim (f(x) — kx)$

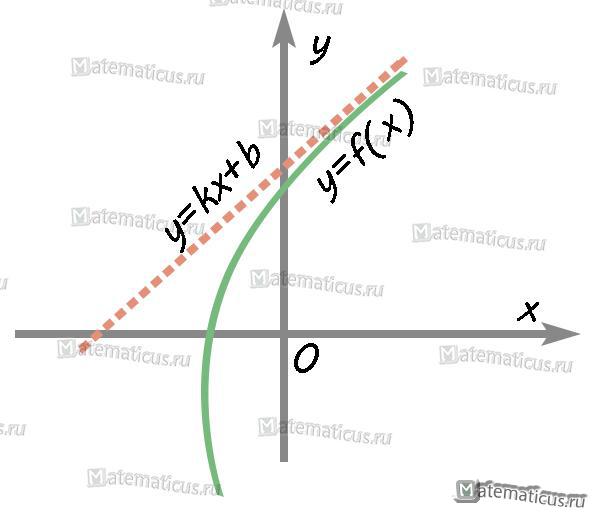
График 3 наклонной асимптоты y=kx+b

---

Пример 1
Найти асимптоты  функции

$y = \frac{{6{x^2} + 5x — 5}}{{2x + 3}}$

Решение

$2x + 3 \ne 0$

$x \ne  — \frac{3}{2}$

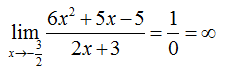
Так как предел равен бесконечности, следовательно получаем вертикальную асимптоту, которая равна

$x =  — \frac{3}{2}$

Найдём наклонную асимптоту функции (это коэффициенты прямой k и b), используя правило Лопиталя, имеем

Прямая имеет вид

y=3x-2

---

Пример 2
Найти асимптоты  функции

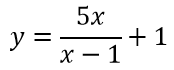
Решение

Преобразуем  данную функцию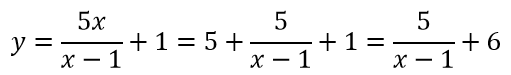

Константа равная 6 показывает, что данная функция поднимется вверх по оси OY и поэтому рассмотрим левую часть данной функции.

Выполняются следующие условия: 

x-1≠0 

x≠1

тогда

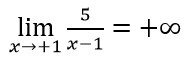
следовательно, функция имеет вертикальную асимптоту x=1.