Найти наибольшее и наименьшее значение функции на интервале

Найти наибольшее и наименьшее значение функции

$y=\frac{x^{3}}{3}-\frac{x^{2}}{2}-2x+1$

на интервале x∈[0;5]
Найдите сумму наибольшего и наименьшего значений функции.

---

Решение
Найдем производную функции

$y=(\frac{x^{3}}{3}-\frac{x^{2}}{2}-2x+1)’=$

=x²–x–2

Приравняем полученное уравнение к нулю, найдем корни квадратного уравнения:

x²–x–2=0

Корни уравнения можно найти через дискриминант или по теореме Виета
Корни уравнения:

x₁=-1; x₂=2

Корень x₁=-1 в интервал не входит, поэтому рассматривать его не будем.
Найдем значения функции на концах интервала и при x₂=2, подставив в функцию

f(5)=$\frac{5^{3}}{3}-\frac{5^{2}}{2}-5*2+1$=20,1666

f(0)=$\frac{0^{3}}{3}-\frac{0^{2}}{2}-0*2+1$=1

f(2)=$\frac{2^{3}}{3}-\frac{2^{2}}{2}-2*2+1$=–2,333

Итак получаем решение
Максимальное значение функции в точке

M_max(5;20,1666)

Минимальное значение функции в точке

M_min(2;-2,333)

Сумма наибольшего и наименьшего значений равна

20,1666+(-2,333)=17,8333

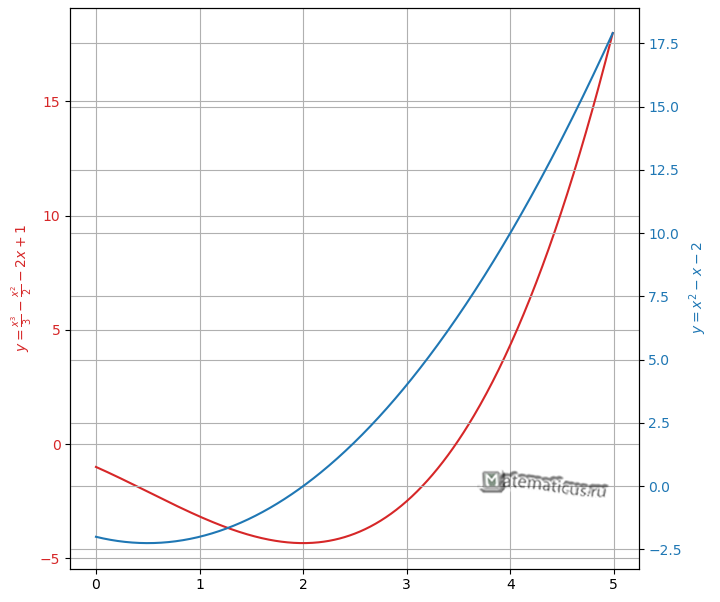
График функции и её производная