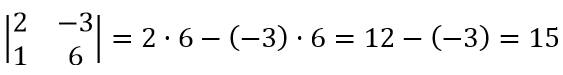Выражение вида:
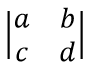
называется определителем второго порядка.
Определитель матрицы обозначается квадратными скобками.
Формула для нахождения определителя второго порядка:
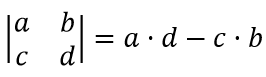
Определитель второго порядка имеет геометрическую интерпретацию — он представляет собой площадь параллелограмма, построенного на векторах-столбцах матрицы. Если определитель равен нулю, это означает, что вектора линейно зависимы, и параллелограмм вырождается в отрезок или даже в точку. Если определитель отличен от нуля, то вектора линейно независимы, и параллелограмм имеет ненулевую площадь.
Свойства определителя второго порядка можно посмотреть здесь.
Пример