С помощью метода Гаусса можно решить любую систему линейных уравнений с различным числом уравнений и неизвестных переменных. И именно этим свойством этот метод превосходит матричный метод и метод Крамера.
Суть метода состоит в приведении системы линейных уравнений к ступенчатому (треугольному) виду за счет последовательного исключения неизвестных. Затем её решения с помощью обратной подстановки.
Допустимые преобразования матрицы:
- Перестановка местами двух строк или двух столбцов;
- Умножение строки на число, которое не равно 0;
- Прибавление одной строки к другой.
- Исключение или добавление нулевой строки
Допустим, дана система линейных алгебраических уравнений с четырьмя уравнениями и четырьмя неизвестными.
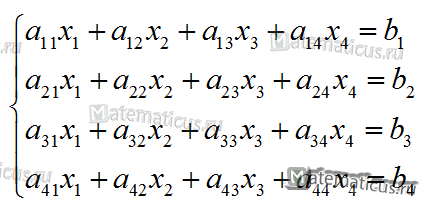
Составим расширенную матрицу СЛАУ:

Затем первое уравнение СЛАУ делим на a11. При этом a11≠0, если равно нуля, то переставляем две строки или два столбца местами так, чтобы избавится от нуля. После полученное уравнение умножаем на a21 и вычитаем из второго уравнения, дальше, умножаем на a31 и вычитаем из третьего уравнения и т.д.
Также поступаем и с оставшемся уравнениями, т.е. со вторым, третьем и четвёртым. В итоге должна получится матрица ступенчатого или треугольного вида.
Система уравнений примет вид
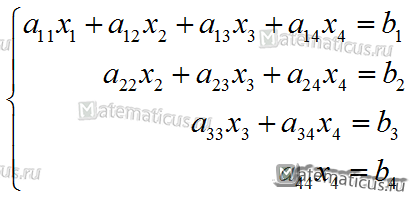
Такую систему элементарно решить обратным ходом, т.е. последовательным решением уравнений от нижнего к верхнему.
Рассмотрим наиболее подробно метод Гаусса при решении СЛАУ на практике.
Пример 1
Решить методом Гаусса систему уравнений
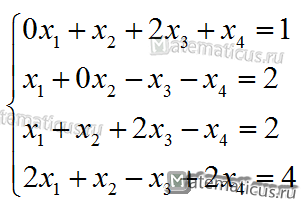
Решение
Составим расширенную матрицу системы уравнений:

Первую строку разделим на a11, но так как в этой строке a11=0, то необходимо поменять строку у которой первый элемент не равен нулю. Выберем по модулю наибольшей элемент, это a41=2 Поэтому поменяем первую и четвёртую строки местами.
Получаем:
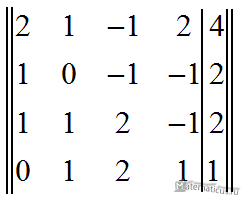
Первую строку разделим на a11=2. Получим матрицу:

Умножаем элементы первой строки на -1 и прибавляем к элементам второй строк. Получим матрицу:
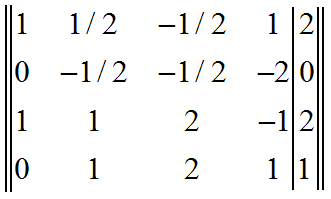
Умножаем элементы первой строки на -1 и прибавляем к элементам третьей строки.
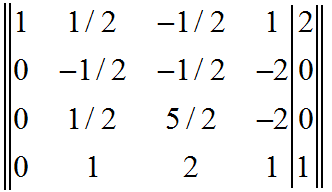
Четвёртую строку оставляем без изменений, так как её первый элемент равен нулю.
Теперь первый столбец не трогаем.
Начинаем повторять действия, которые применяли ранее.
Второе уравнение разделим на a22=-1/2, тогда

Умножаем элементы второй строки на -1/2 и прибавляем к элементам третьей строки.
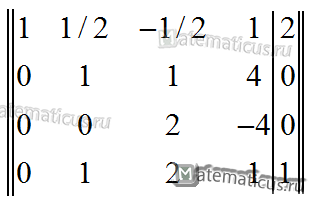
Умножаем элементы второй строки на -1 и прибавляем к элементам четвёртой строки.

Первый и второй столбец не трогаем.
Третьей столбец разделим на 2.

Умножаем элементы третьей строки на -1 и прибавляем к элементам четвёртой строки.

Получаем ступенчатую систему алгебраических уравнений:
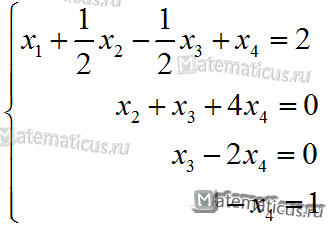
Отсюда, решая систему снизу вверх, получаем корни системы уравнений
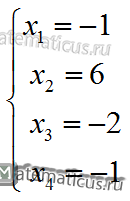
Приведём простой пример краткой записи решения СЛАУ методом Гаусса
Пример 2
Решить систему линейных уравнений с тремя неизвестными методом Гаусса.
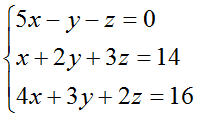
Решение
Составим расширенную матрицу системы линейных уравнений .
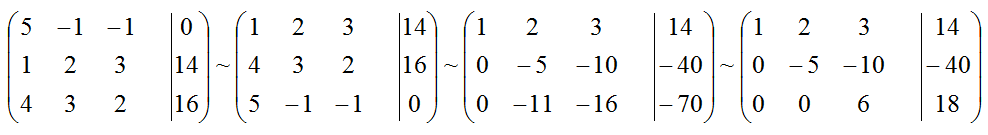
Следовательно, искомая система может быть представлена в ступенчатом виде:
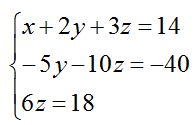
Решая последовательно уравнение, получаем:
Ответ: z = 3; y = 2; x = 1
