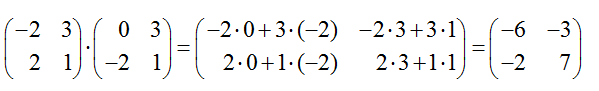Основной принцип умножения матрицы на матрицу заключается в скалярном умножении каждого элемента левой строки матрицы на каждый элемент правого столбца  матрицы. В общем виде, математически можно записать формулу в следующем виде:

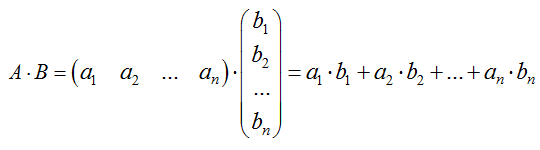
A — левая матрица;

B — правая матрица.

При умножении матриц должно соблюдаться следующее главное условие:

A_mxn·B_nxk=C_mxk

m — строка, k — столбец

Если это условие не соблюдается, то матрицы нельзя перемножать.

Свойства операции умножения матриц

1. (A·B)·C=A·(B·C)=A·B·C
2. (A+B)·C=A·C+B·C
3. A·B≠B·A
4. α·(A·B)=(α·A)·B=A·(α·B), где  α — число
5. A_mxn·E_n=E_m·A_mxn=A_mxn, где A_mxn — единичная матрица

---

Пример 1

Дана матрица A и B

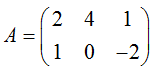
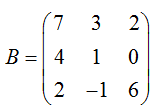
Найти произведение матрицы на матрицу AB и BA

Решение

Произведения матрицы на матрицу  BA не существует. Число столбцов матрицы B не одинаково с числом строк матрицы A, т.е. 3≠2.

Пример 2

A=(4    2    -1)

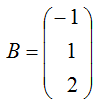
Найти AB и BA.

Решение

A=4·(-1)+2·1+(-1)·2)=-4

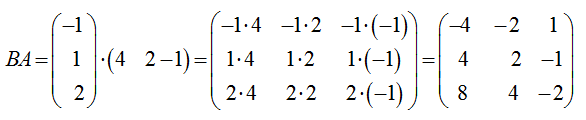
Пример с решением 3

Умножение квадратной матрицы два на два: