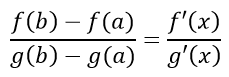Теорема Ролля (теорема о нуле производной)
Если функция у = f(x) непрерывна на отрезке [а, b], дифференцируема на интервале (а,b) и при этом f(а)=f(b), тогда внутри отрезка [а, b] существует хотя бы одна точка x0=С, в которой производная равна нулю
f'(С) = 0
Геометрическая интерпретация теоремы Ролля:
На графике функции найдется такая точка, в которой касательная к графику параллельна оси ОХ.
Теорема Лагранжа (теорема о конечных приращениях)
Если функция у = f(x) непрерывна на отрезке [а, b], дифференцируема на интервале (а,b), тогда существует хотя бы одна точка, такая что:
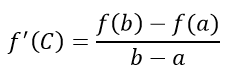
Геометрическая интерпретация теоремы Лагранжи:
tg(α)=f'(С)
Теорема Коши (теорема об отношении приращений)
Если функция f(x) и g(x) непрерывна на отрезке [а, b], дифференцируема на интервале (а,b), g(x)≠0 на интервале (а,b), тогда существует хотя бы одна точка x (a<x<b), такая что: