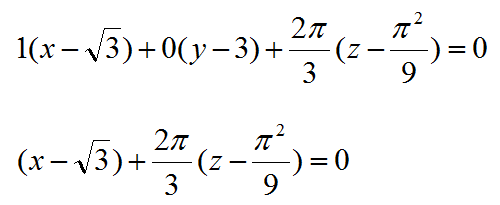Уравнение нормальной плоскости к кривой

Уравнение нормальной плоскости к кривой имеет вид:

---

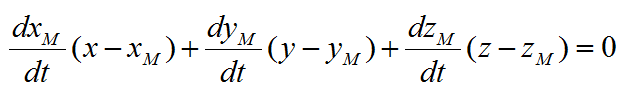
Пример

Составить уравнение нормальной плоскости к кривой

 

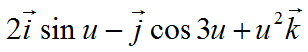
в точке $\frac{\pi}{3}$

Решение

Из условия задачи, уравнения по осям координат

x(u)=2sinu

y(u)=–cos3u

z(u)=u

Найдем производные в точке $\frac{\pi}{3}$

x′(u)=(2sinu)′=2cosu

y′(u)=(–cos3u)′=3sin3u

z′(u)=(u²)′=2u

x′($\frac{\pi}{3}$) =2cos($\frac{\pi}{3}$)=1

y′($\frac{\pi}{3}$)==3sin3($\frac{\pi}{3}$)=0

z′($\frac{\pi}{3}$)= $\frac{2\pi}{3}$

x($\frac{\pi}{3}$) =2sin($\frac{\pi}{3}$)=$\sqrt{3}$

y($\frac{\pi}{3}$)= -3cos3($\frac{\pi}{3}$)=3

z($\frac{\pi}{3}$)= $(\frac{\pi}{3})^{2}$