Интегральный признак Коши определяется из следующего условия:
если элементы ряда $\mathop \sum \limits_{n = 1}^\infty {u_n}$ — положительны и для которого существует функция f(x) — непрерывная, положительная, монотонно убывающая на интервале [1; ∞] и f(n)=un
Следовательно ряд
$\mathop \sum \limits_{n = 1}^\infty {u_n}$
и несобственный интеграл
$\mathop \smallint \limits_1^{ + \infty } f\left( x \right)dx$
одинаково сходятся и расходятся.
Пример
Ряд вида
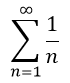
расходится
Проверим этот ряд по интегральному признаку Коши
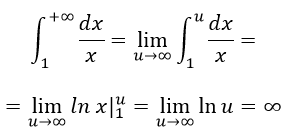
Получаем ∞, следовательно ряд расходится.
См. также
