Признак Лейбница о сходимости ряда

Пусть имеется знакочередующийся ряд вида:

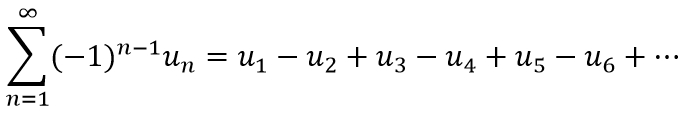
Этот ряд по признаку Лейбница будет сходится при условиях:

1. u₁>u₂>u₃>u₄>u₅>…>u_n>…, т.е. последовательность модулей членов ряда убывает

2.

Тогда ряд сходится, но при этом надо учитывать, что сумма ряда должна удовлетворять следующему условию:

0<S<u₁

где

S – сумма ряда.

---

Пример

Исследовать на сходимость знакочередующейся ряд:

$$1 — \frac{1}{2} + \frac{1}{3} — \frac{1}{4} + … = \sum\limits_{n = 1}^{ + \infty } {{{\left( { — 1} \right)}^{n + 1}}} \frac{1}{n}$$

Решение

Воспользуемся признаком Лейбница.

Абсолютные величины монотонно убывают:

$$\left\{ {\left| {{{\left( { — 1} \right)}^{n + 1}}\frac{1}{n}} \right|} \right\} = \left\{ {\frac{1}{n}} \right\}$$

$$1 > \frac{1}{2} > … > \frac{1}{n} > … > 0$$

$$\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0$$

Из этого следует, что ряд

$$1 — \frac{1}{2} + \frac{1}{3} — \frac{1}{4} + … = \sum\limits_{n = 1}^{ + \infty } {{{\left( { — 1} \right)}^{n + 1}}} \frac{1}{n}$$

сходится.