Тригонометрический ряд Фурье

Тригонометрический ряд Фурье это функциональный ряд, который представляется выражением:

$\frac{a_0}{2}+a_1cosx+a_1sinx+a_2cosx+a_2sinx+…+a_ncosx+a_nsinx$

Тригонометрический ряд Фурье для функции с периодом 2π вычисляется по формуле:

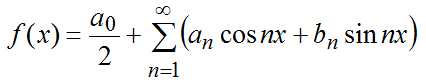
Коэффициенты тригонометрического ряд Фурье находятся по формулам:

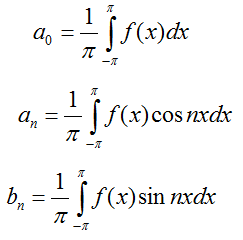
Если функция f(x) задана на нечётном полупериоде, то получаем ряд с синусами:

 

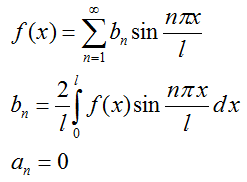
Если функция f(x) задана на чётном полупериоде, то получаем ряд с косинусами:

---

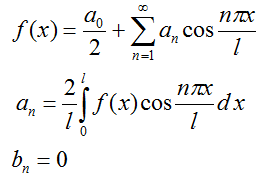
Пример
Разложите в ряд Фурье функцию

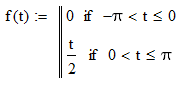
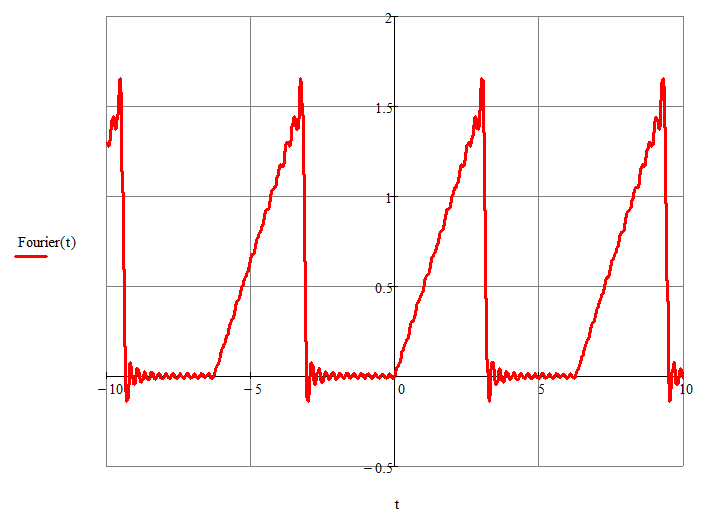
График функции
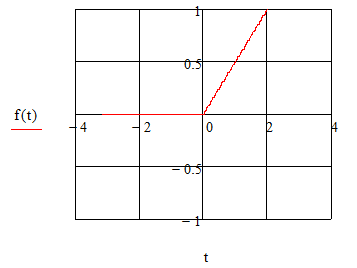Решение

Для разложения функции в тригонометрический ряд Фурье воспользуемся формулами выше, тогда

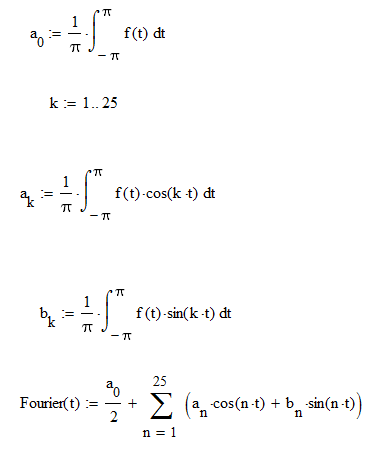
Получаем график искомой функции в виде тригонометрического ряда Фурье