Биномиальный  закон распределения случайной величины

Распределение вероятностей называется биномиальным, если вычисляется по формуле Бернулли:

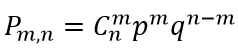
 $C_n^m$ — число сочетаний m по n, находится по формуле здесь.

p — вероятность наступления события;
q=p-1 — вероятность не наступления события

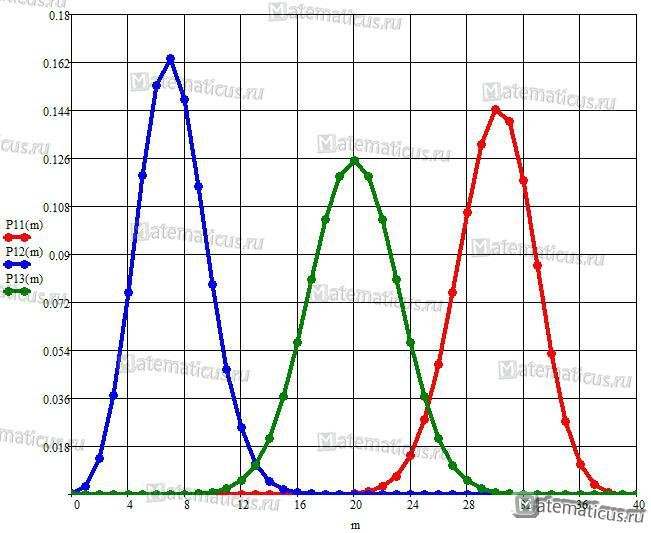
График плотности распределения для биномиального закона распределения СВ.

при k=30, p=0.75
при k=30, p=0.18
при k=30, p=0.5

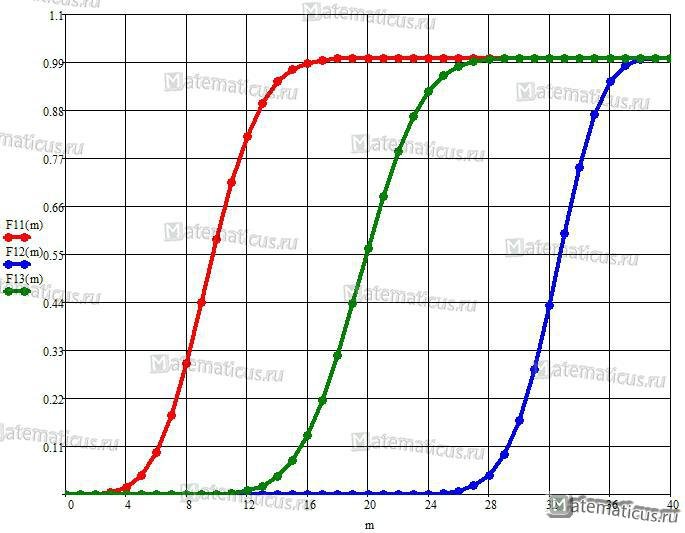
График функции распределения

Биномиальное распределение относится к дискретному распределению.

Математическое ожидание для этого распределения имеет вид:

  M(X)=n⋅p

Дисперсия равна:

  D(X)=n⋅p⋅q

Ряд биномиального закона распределения дискретной случайной величины в виде таблицы:

---

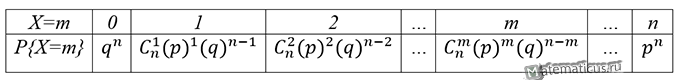
Пример 1

Тракторный завод получает два госзаказа на производство тракторов из 10. Необходимо составить закон распределения вероятностей на производство m тракторов, построить полигон распределения вероятностей.

Решение
Из условия получаем
p=2/10=0,2
q=1-p=1-0,2=0,8
n=10

m	$C_n^m$	pm	qn-m	Pm,n
0	1	1,0000000000	0,348678	0,3486784401
1	10	0,1000000000	0,38742	0,3874204890
2	45	0,0100000000	0,430467	0,1937102445
3	120	0,0010000000	0,478297	0,0573956280
4	210	0,0001000000	0,531441	0,0111602610
5	252	0,0000100000	0,59049	0,0014880348
6	210	0,0000010000	0,6561	0,0001377810
7	120	0,0000001000	0,729	0,0000087480
8	45	0,0000000100	0,81	0,0000003645
9	10	0,0000000010	0,9	0,0000000090
10	1	0,0000000001	1	0,0000000001

Полигон распределения вероятностей будет иметь вид:

---

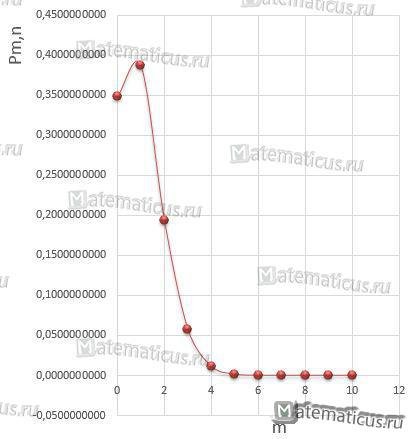
Пример 2

Производится три выстрела по мишени, вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти ее ряд распределения.

Решение

Здесь, n = 3;

p = 0,8 — вероятность попадания;

q = 1 — 0,8 = 0,2 — вероятность промоха

Для вычисления применим формулу

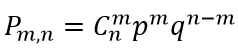
получим

${P_3}\left( 0 \right) = P\left( {X = 0} \right) = C_3^0{0,8^0}{0,2^{3 — 0}} = {0,2^3} = 0,008$

${P_3}\left( 1 \right) = P\left( {X = 1} \right) = C_3^1{0,8^1}{0,2^{3 — 1}} = 3 \cdot {0,2^2} \cdot 0,8 = 0,096$

${P_3}\left( 2 \right) = P\left( {X = 2} \right) = C_3^2{0,8^2}{0,2^{3 — 2}} = 3 \cdot 0,2 \cdot {0,8^2} = 0,384$

${P_3}\left( 3 \right) = P\left( {X = 3} \right) = C_3^3{0,8^3}{0,2^{3 — 3}} = {0,8^3} = 0,512$

Представим графически в виде гистограммы

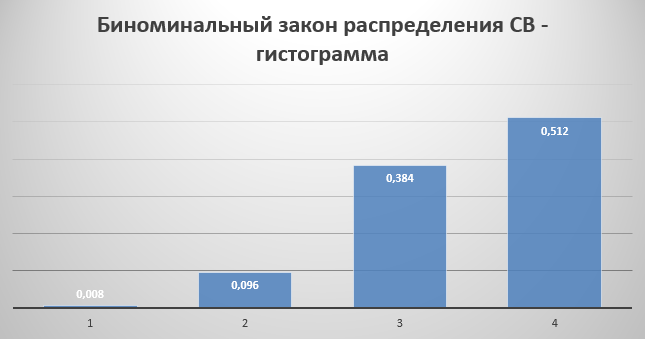
Ряд распределения случайной величины имеет вид:

X	0	1	2	3
P	0.008	0.096	0.384	0.512

Проверяем:

∑p=0,008+0,096+0,384+0,512=1