Гамма распределение

Случайная величина X имеет гамма-распределение с параметрами, если ее плотность распределения вероятностей имеет вид при этом параметры λ>0 и k>0:

 

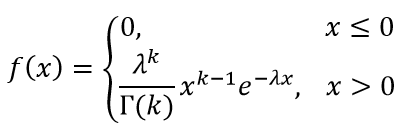
где

λ, k —  параметры распределения

Г(k) — гамма функция Эйлера, которая находится по формуле:

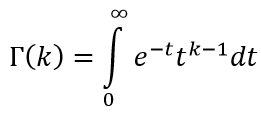
Вид графика плотности бета-распределения в виде гистограммы при α=2  β=22 со смещением по оси ОX на 100 единиц вправо.

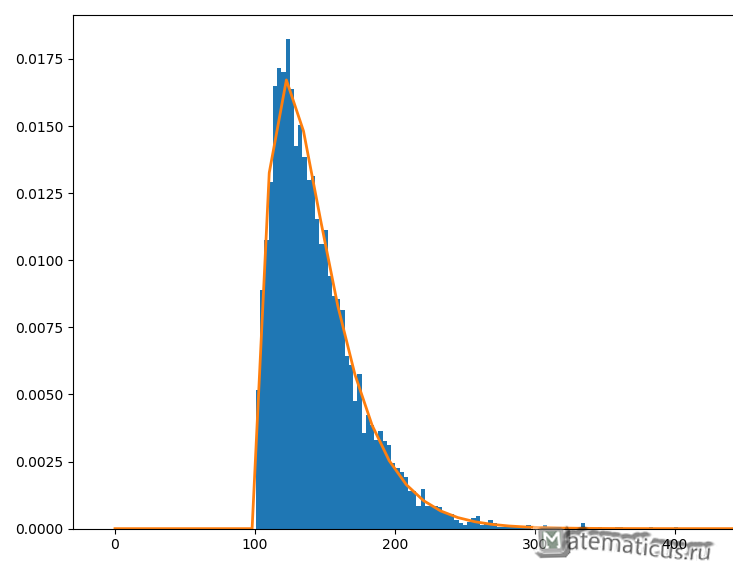
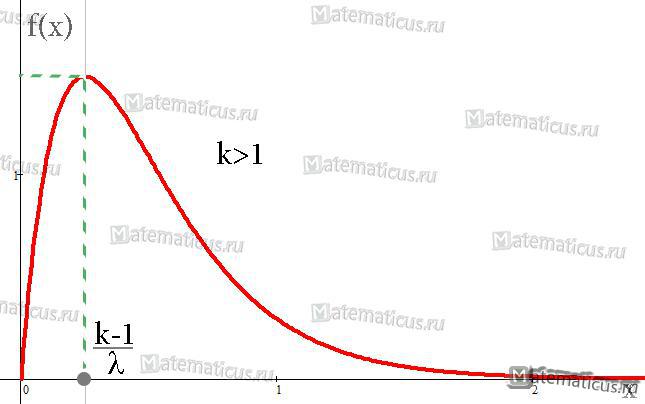
Рисунок 1 — График плотности распределения при k>1

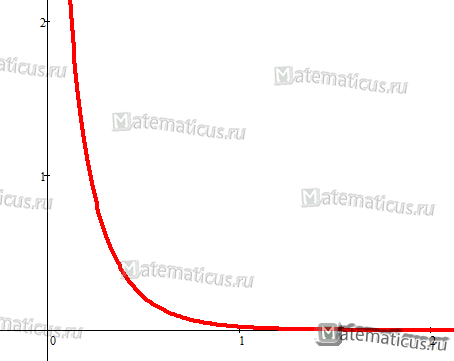
Рисунок 2 — График плотности распределения при k<1

При k=1 — Гамма распределение принимает экспоненциальное распределение.

При k>1 и целых значениях k гамма-распределение преобразуется в распределение Эрланга k-ого порядка.

Математическое ожидание:

M(X)=k/λ

Дисперсия находится из выражения:

D(x)=k/λ²

Мода равна:

M₀=(k-1)/λ

Второй начальный момент равен:

D(x)=k(k+1)/λ²