Дискретная случайная величина X имеет гипергеометрическое распределение, если ее закон распределения имеет следующий вид:
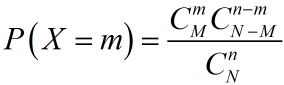
Этот закон распределения показывает вероятность того, что среди n отобранных изделий будет ровно m стандартных.
N — общее количество изделий;
M — количество стандартных изделий;
m=0, 1, 2,…, min (M,n)
Примечание
Отобранные изделия не возвращаются в партию
Формула для определения математического ожидания:
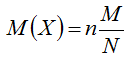Формула дисперсии:
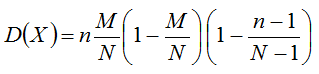
или
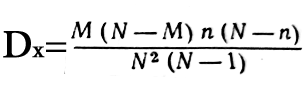
Пример 1
Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наудачу извлеченных 5 изделий окажется ровно 3 окрашенных.
Решение
Здесь N = 50, M = 20, n = 5, m = 3.
Тогда вероятность равна:
$P\left( {X = 3} \right) = \frac{{C_{20}^3C_{30}^2}}{{C_{50}^5}} = 0,234$
Пример 2
В корзине 55 шариков, пронумерованы от 1 до 55. Составить закон распределения восьми угаданных шариков.
Решение
Всего шариков N=55, угадать требуется n=8 шариков.
m — количество угаданных шариков.
Для составления закон распределения составим вспомогательные таблицы:
| n | M | N | N-M |
| 8 | 8 | 55 | 47 |
| n-m | m | $C_M^m$ | $C_{N — M}^{n — m}$ | $C_N^n$ | P |
| 8 | 0 | 1 | 314457495 | 1217566350 | 0,2582672353 |
| 7 | 1 | 8 | 62891499 | 1217566350 | 0,4132275765 |
| 6 | 2 | 28 | 10737573 | 1217566350 | 0,2469286737 |
| 5 | 3 | 56 | 1533939 | 1217566350 | 0,0705510496 |
| 4 | 4 | 70 | 178365 | 1217566350 | 0,0102545130 |
| 3 | 5 | 56 | 16215 | 1217566350 | 0,0007457828 |
| 2 | 6 | 28 | 1081 | 1217566350 | 0,0000248594 |
| 1 | 7 | 8 | 47 | 1217566350 | 0,0000003088 |
| 0 | 8 | 1 | 1 | 1217566350 | 0,0000000008 |
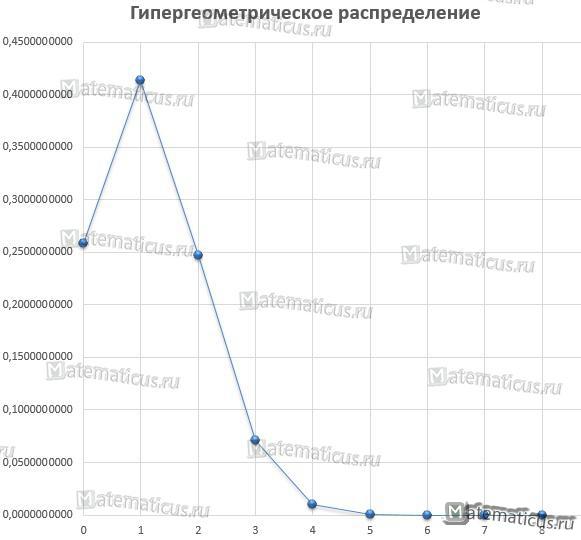
На графике видно, что вероятность угадывания первого шарика превосходит над вероятностью не угадывания, т.е. P(m=1)>P(m=0). Вероятность угадывания от 5 P(m=5) и более шариков стремится к нулю.
2858