Плотность распределения закона Эрланга определяется выражением:
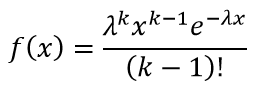
Математическое ожидание определяется по формуле:
$M(X) = \frac{k}{\lambda }$
Дисперсия равна:
$D(X) = \frac{k}{{{\lambda ^2}}}$
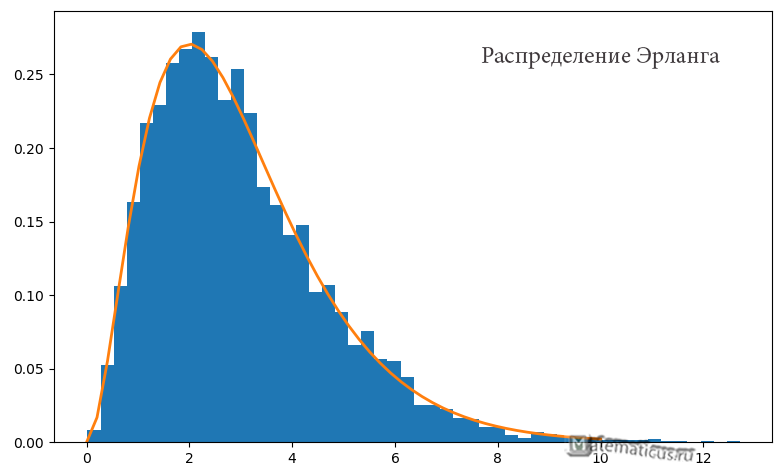
Гистограмма распределения Эрланга при k=3 и λ=1
При k=1 распределение Эрланга преобразуется в показательное (экспоненциальное) распределение СВ с параметром λ.
При k>1 и целых значениях k гамма-распределение преобразуется в распределение Эрланга k-ого порядка.
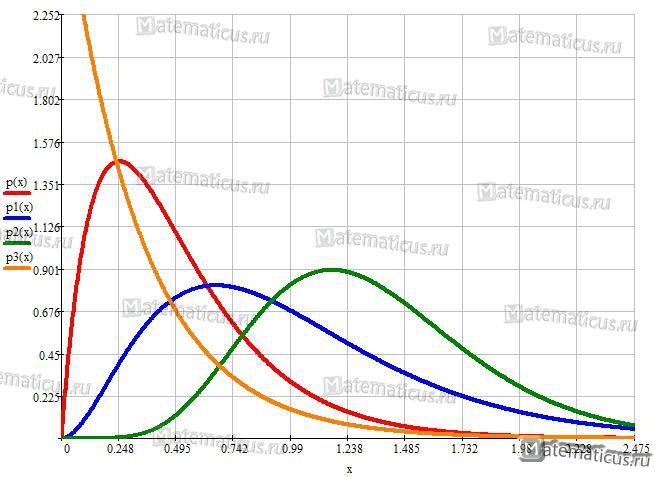
График плотности распределения случайной величины Эрланга при λ=4 и k=2, λ=3 и k=3, λ=6 и k=8, λ=3 и k=1
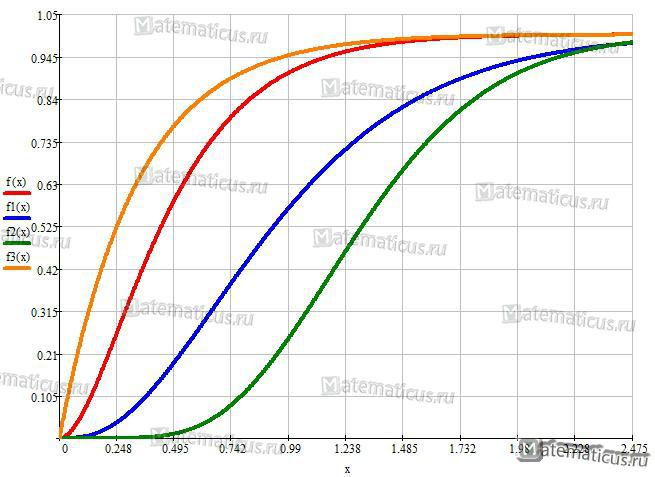
График функции распределения случайной величины Эрланга при λ=4 и k=2, λ=3 и k=3, λ=6 и k=8, λ=3 и k=1
Закон распределения случайной величины Эрланга применяется в теории массового обслуживания, например, временной простой общественного транспорта на остановках, моменты поступления грузовых автомобилей на склад стройматериалов и т.д.
