Распределение Пирсона хи-квадрат

Распределение χ² Пирсона

Плотность вероятности находится через уравнение:

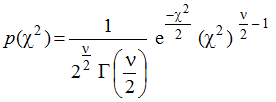
ν — параметр, определяет число степеней свободы распределения и является целым положительным числом;

Г — Гамма-функция Эйлера второго порядка.

Для чётных функций функция Эйлера определяется выражением:

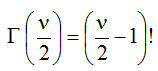
для нечётных функций:

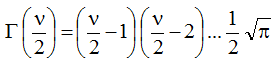
Функция вероятности определяется уравнением:

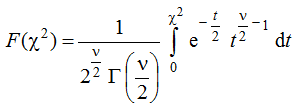
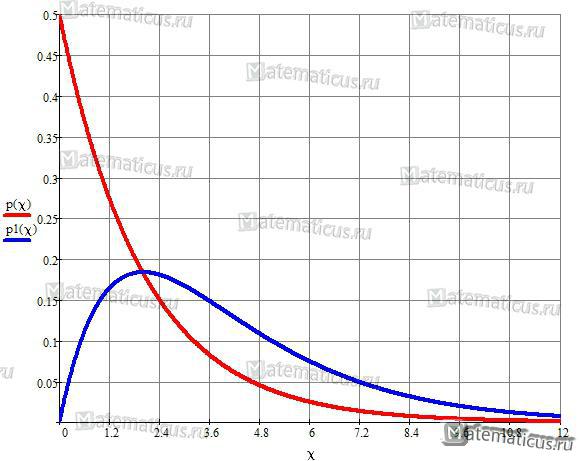
График плотности распределение χ² Пирсона при ν=2 и ν=4

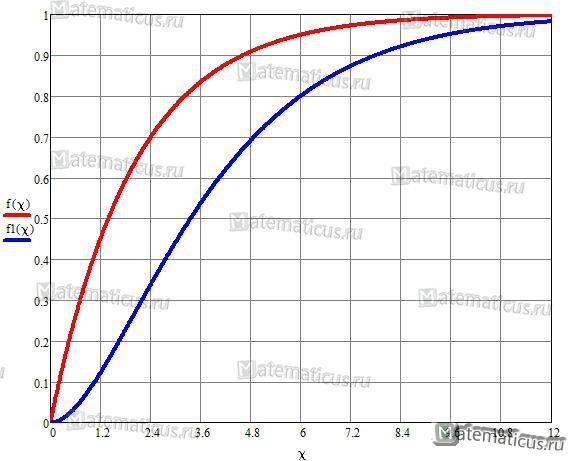
График функции распределение χ² Пирсона при ν=2 и ν=4

Математическое ожидание равно:

M_x=ν

Дисперсия равна:

D_x=2ν

Формула моды:

M₀=ν-2

Стандартное отклонение равно:

$$\sigma = \sqrt {2\,\nu } $$

При больших значениях параметра  ν распределения χ² Пирсона стремится к нормальному закону распределения СВ.

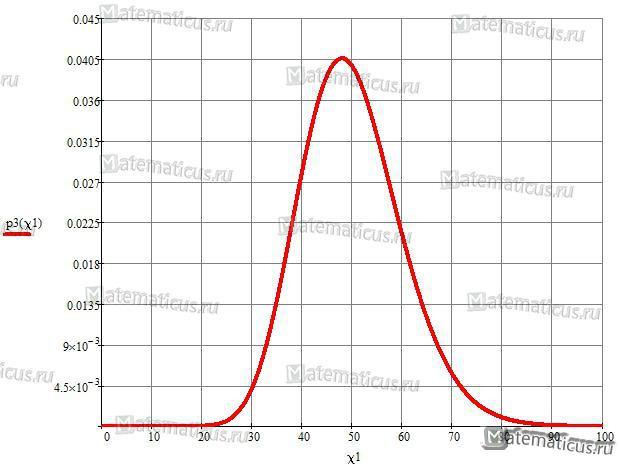
График плотности распределение χ² Пирсона при ν=50