Функция плотности вероятности распределение Стьюдента (t-распределение) определяется выражением:
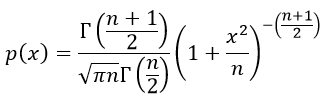
n — число степеней свободы, является параметром распределение Стьюдента.
Γ(y) — гамма-функция.
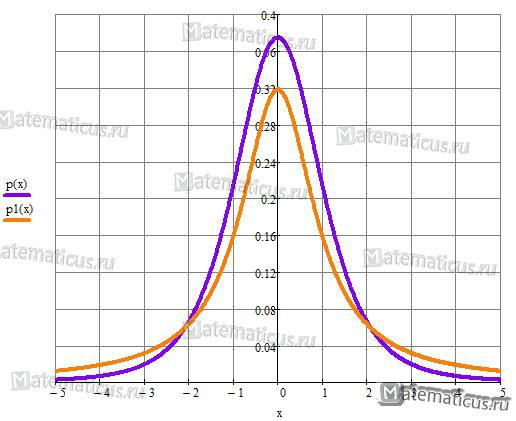
График плотности вероятности при n=4 и n=1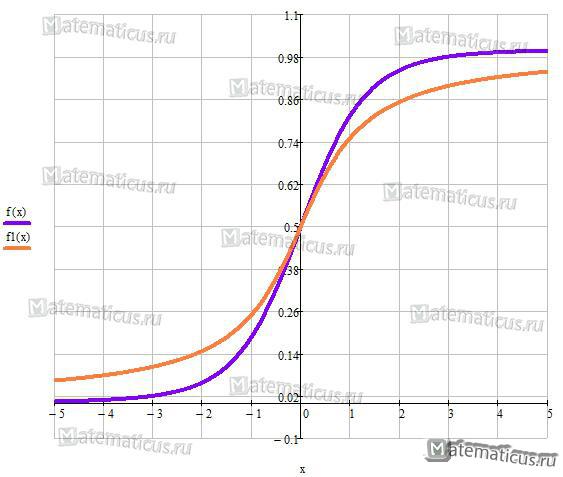
График функции вероятности n=4 и n=1
При n→∞ распределение Стьюдента приближается к нормальному закону распределения СВ. При n>20 можно использовать нормальный закон распределения.
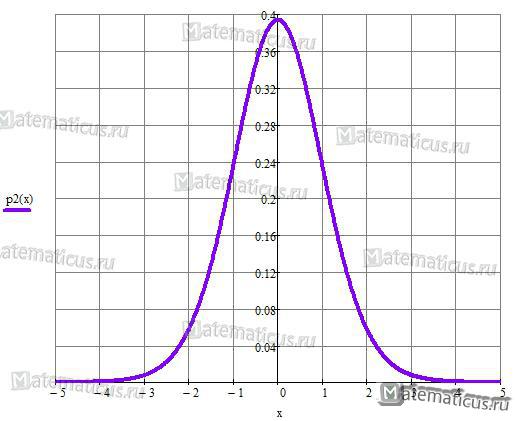
График плотности вероятности при n=20
Основные характеристики t-распределения при области значений (-∞; ∞):
Математическое ожидание и мода равны нулю.
Mx=0, M0=0 если n>0
Dx=n/n-2, если n>2
Асимметрия A=0, если n>3
Эксцесс E=6/n-4, если n>4
