Закон равномерного движения
Случайную величину равномерно распределённой на интервале (a, b) и её плотность вероятности равна некоторой постоянной величине на этом интервале и нулю вне него.
a, b — параметры распределения.
Таким образом, случайная непрерывная величина X имеет равномерное распределение, если она принимает значения хi (где i=1…n, n — независимые испытания) с одинаковыми вероятностями,
$p\left( {{x_i}} \right) = \frac{1}{n}$
Случайная величина X на промежутке от а до b имеет равномерное распределение, если плотность распределение равна
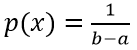
на заданном промежутке, а вне его р(х)=0
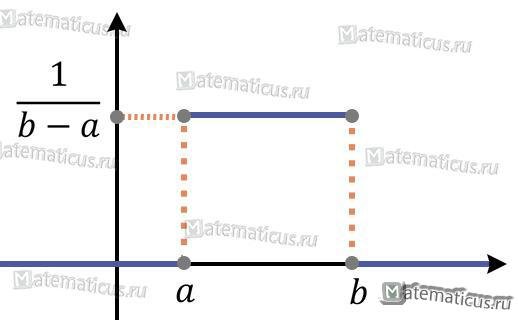
График плотности вероятности
или плотность распределения можно записать в виде:
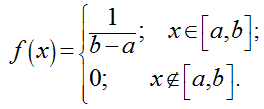
Функция распределения в этом случае имеет вид:
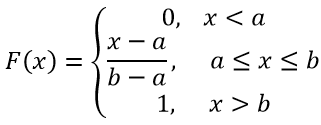
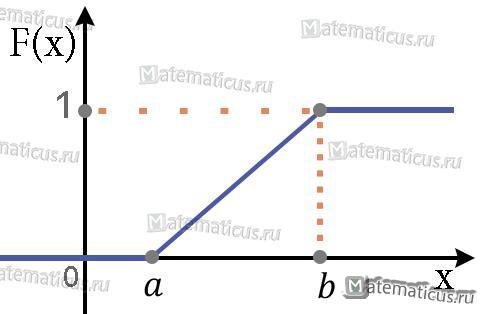
График функции распределения
Математическое ожидание случайной непрерывной величины X вычисляется следующим образом:
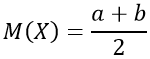
Математическое ожидание получается из выражения:
\[M\left( X \right) = \int\limits_a^b {xf\left( x \right)dx = \frac{1}{{\left( {b — a} \right)}}\int\limits_a^b {xdx = \left. {\frac{{{x^2}}}{{2\left( {b — a} \right)}}} \right|} _a^b = \frac{{{b^2} — {a^2}}}{{2\left( {b — a} \right)}} = \frac{{\left( {b + a} \right)}}{2}} \]
Дисперсия случайной непрерывной величины X вычисляется следующим образом:
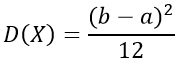
Дисперсия выводится из выражения:
$D\left( X \right) = \int\limits_a^b {{x^2}f\left( x \right)dx — {{\left[ {M\left( X \right)} \right]}^2} = \frac{1}{{\left( {b — a} \right)}}} {\int\limits_a^b {{x^2}dx — \left[ {\frac{{a + b}}{2}} \right]} ^2} = $
$=\left. {\frac{{{x^3}}}{{3\left( {b — a} \right)}}} \right|_a^b — {\left[ {\frac{{a + b}}{2}} \right]^2} = \frac{{{a^2} + ab + {b^2}}}{3} — {\left[ {\frac{{a + b}}{2}} \right]^2}= \frac{{{{\left( {b — a} \right)}^2}}}{{12}}$
Среднее квадратическое отклонение (СКО) равно:
\[\sigma \left( X \right) = \sqrt {D\left( X \right)} = \sqrt {\frac{{{{\left( {b — a} \right)}^2}}}{{12}}} = \frac{{\left( {b — a} \right)\sqrt 3 }}{6}\]
Медиана равна:
$\frac{{a + b}}{2}$
Мода:
Любое число из отрезка [a, b]
Пример 1
Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 10 с.
В условии задачи, случайная непрерывная величина X — это показание часов, которая соответствует равномерному закону распределения СВ в диапазоне от 0 секунд до 60 секунд.
Вычислим плотность распределения данной СВ:
$p\left( x \right) = \frac{1}{{60 — 0}} = \frac{1}{60}$
Это событие может произойти либо в интервале (0; 10), либо в интервале (50; 60), то есть стрелка может переместиться как вправо, так и влево на на 10 с и данные два события независимые. По теореме сложения, получаем
Р(0<X<10)+Р(50<X<60)
Подставляя значения в формулу, имеем
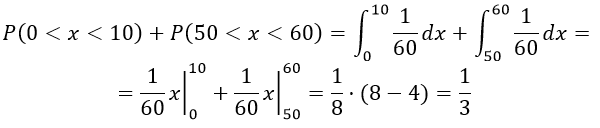
Пример 2
Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете
будет сделана ошибка:
а) меньшая 0,04;
б) большая 0,05
Решение
а) Найдем вероятность того, что при отсчете будет сделана ошибка меньшая 0,04 через интеграл:
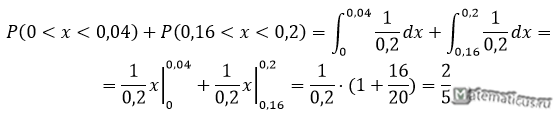
б) Аналогично, большая 0,05
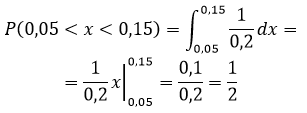
Пример 3
Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин.
Решение
Плотность распределения равномерной случайной величины равна:
$p\left( x \right) = \frac{1}{{5 — 0}} = \frac{1}{5}$
Вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин равна:
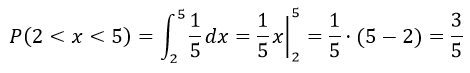
Пример 4
Ребро куба х измерено приближенно, причем а≤х≤b. Рассматривая ребро куба как случайную величину X, распределенную равномерно в интервале (а;b), найти математическое ожидание и дисперсию объема куба.
Решение
Плотность распределения случайной величины равна:
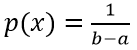
В виду того, что X3 , тогда математическое ожидание:
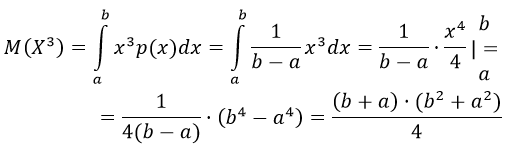
Найдём дисперсию:

