Закон распределения случайной величины Пуассона 

Закон распределения СВ Пуассона вытекает из биномиального закона распределения СВ и относится к дискретному распределению.

В случая малых значений р→0 (то есть при р≤0,1) и большом значении n→∞ применяется закон распределения случайной величины Пуассона.

Вероятность того, что случайная величина X примет значение равное k, вычисляется по формуле:

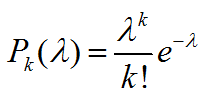
  Р(Х=k) = P_n(k) = λ^k⋅e^-λ/k!

где  λ=n⋅p = const

Это выражение описывает плотность вероятности.

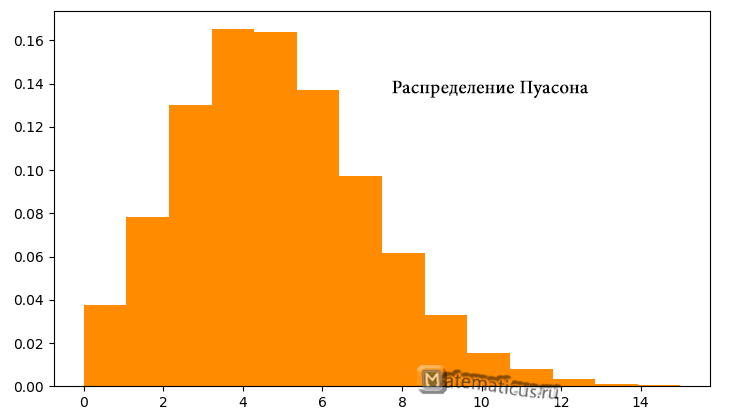
Таблица ряда распределения случайной величины X по закону Пуассона:


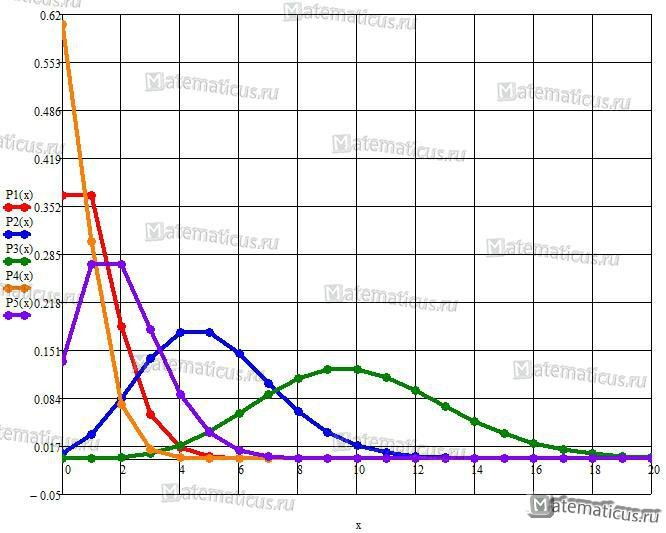
График плотности распределения случайной величины, где красным цветом при λ=1, синим λ=5, зелёным λ=10, оранжевым λ=0.5 и фиолетовым λ=2
Функция распределения определяется равенством:


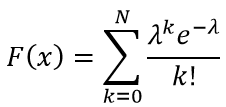
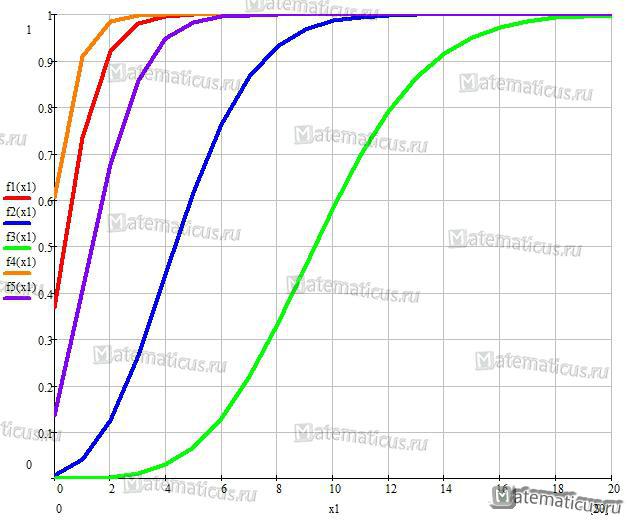
График функции распределения случайной величины по закону Пуассона при λ=1, λ=5, λ=10, λ=0.5 и λ=2
Закон распределения Пуассона связан с редкими событиями, например, число дефектов в производственном процессе, число несчастных случаев и т д. Применяется также системах массового обслуживания.
Параметр распределения равен:   λ
Математическое ожидание:

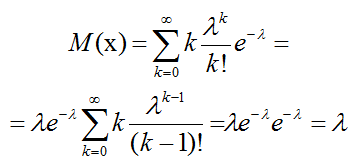
M(x) = λ

Дисперсия:

$D(X) = M({X^2}) — {M^2}(X)$ 

$$M(x) = \lambda  \Rightarrow {M^2}(x) = {\lambda ^2}$$

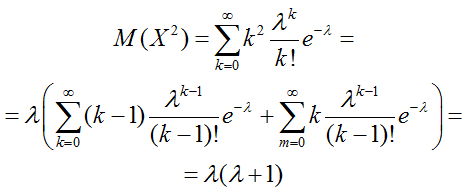
$\displaylines{D(X) = M({X^2}) — {M^2}(X) =  \cr = \lambda (\lambda  + 1) — {\lambda ^2} = \lambda  \cr} $

D(x) = λ

---

Пример
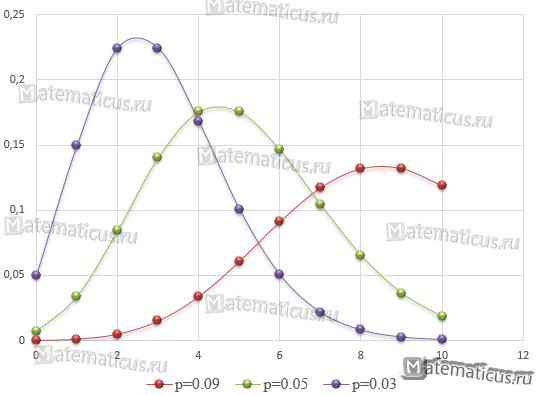
В магазин по продажи холодильников поступает примерно 100 звонков в день. Вероятность того, что закажут холодильник белого цвета 0,09; чёрного — 0,07 и бежевого — 0,03.
Требуется составить закон распределения заказов на покупку холодильников.
Решение
Здесь n=100 и p₁=0,09, p₂=0,07, p₃=0,03. 
Так как λ=np, тогда
λ₁=9, λ₂=7 и λ₃=3
Составим таблицу распределения вероятностей при различных значениях k и λ.

k	λ1=9	λ2=5	λ3=3
0	0,000123	0,006738	0,049787
1	0,001111	0,03369	0,149361
2	0,004998	0,084224	0,224042
3	0,014994	0,140374	0,224042
4	0,033737	0,175467	0,168031
5	0,060727	0,175467	0,100819
6	0,09109	0,146223	0,050409
7	0,117116	0,104445	0,021604
8	0,131756	0,065278	0,008102
9	0,131756	0,036266	0,002701
10	0,11858	0,018133	0,00081

На основании этой таблицы построим полигон распределения покупки холодильников.